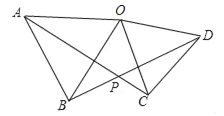
【题目】已知:如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50°.
求证:(1)AC=BD;
(2)∠APB=50°.
参考答案:
【答案】(1)答案见解析;(2)答案见解析.
【解析】整体分析:
利用SAS证明△AOC≌△BOD,则有AC=BD,结合三角形的内角的定理即可求证∠APB=50°.
证明:①∵∠AOB=∠COD=50°,
∴∠AOB+∠BOC=∠COD+∠BOC,
∴∠AOC=∠BOD.
在△AOC和△BOD中,
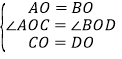
∴△AOC≌△BOD(SAS),
∴AC=BD.
②∵△AOC≌△BOD,
∴∠OAC=∠OBD,
∴∠OAC+∠AOB=∠OBD+∠APB,
∴∠OAC+50°=∠OBD+∠APB,
∴∠APB=50°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】①如果两个数的和为1,则这两个数互为倒数;
②如果两个数积为0,则至少有一个数为0;
③绝对值是它本身的有理数只有0;
④倒数是它本身的数是﹣1,0,1.
其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=(x-1)2-4,AB为半圆的直径,求这个“果圆”被y轴截得的弦CD的长.
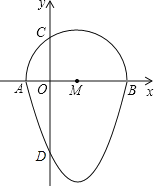
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC平分∠DAB,CE⊥AB于点E,AB=AD+2BE,则下列结论:①AE=
 (AB+AD);②∠ADC+∠B=180°;③CD=CB;④SACE﹣SBCE=SACD.其中正确的是______.
(AB+AD);②∠ADC+∠B=180°;③CD=CB;④SACE﹣SBCE=SACD.其中正确的是______.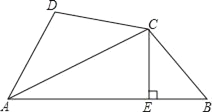
-
科目: 来源: 题型:
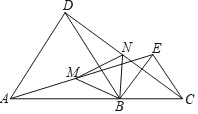
查看答案和解析>>【题目】如图,点A、B、C在同一直线上,△ABD,△BCE都是等边三角形.
(1)求证:AE=CD;
(2)若M,N分别是AE,CD的中点,试判断△BMN的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式m2+m+1=0,那么代数式2018﹣2m2﹣2m的值是( )
A.2016
B.﹣2016
C.2020
D.﹣2020 -
科目: 来源: 题型:
查看答案和解析>>【题目】长为9,6,5,4的四根木条,选其中三根组成三角形,选法有( )
A.1种 B.2种 C.3种 D.4种
相关试题

