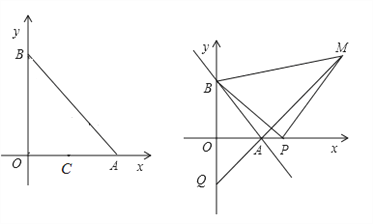
【题目】如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足![]()
(1)求A、B两点的坐标;
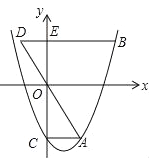
(2)C为OA的中点,作点C关于y轴的对称点D,以BD为直角边在第二象限作等腰Rt△BDE,过点E作EF⊥x轴于点F.若直线y=kx-4k将四边形OBEF分为面积相等的两部分,求k的值;
(3)如图,P为x轴上A点右侧任意一点,以BP为边作等腰Rt△PBM,其中PB=PM,直线MA交y轴于点Q,当点P在x轴上运动时,线段OQ的长是否发生变化?若不变,求其值;若变化,求线段OQ的取值范围.
参考答案:
【答案】(1)A(4,0),B(0,4);(2)k值为![]() 或-
或-![]() 或
或![]() ;(3)见解析
;(3)见解析
【解析】(1)首先根据已知条件和非负数的性质得到关于a、b的方程,解方程组即可求出a,b的值,也就能写出A,B的坐标;
(2)先判段出△DEF≌△BDO,得出EF、OF,即可求出四边形OBEF的面积为18,再分析两种情况可讨论计算即可.
(3)过M作x轴的垂线,通过证明△PBO≌△MPN得出MN=AN,转化到等腰直角三角形中即可得出结论.
解:(1)∵![]() ,
,
∴a=4,b=4,
∴A(4,0),B(0,4);
(2)由(1)知,B(0,4);
∴OB=4,
∵C为OA的中点,
∴C(2,0),
∵点C关于y轴的对称点D,
∴D(-2,0)
∴OD=2,
∵BD为直角边在第二象限作等腰Rt△BDE,
①如图,

当BD=BE,∠DBE=90°时,过点E作EH⊥OB于H,
∴∠BHE=90°,
∴∠BEH+∠HBE=90°,
∵∠DBE=90°,
∴∠HBE+∠OBD=90°,
∴∠BEH=∠OBD,
在△OBD和△HEB中,∠BOD=∠EHB=90°,∠0BD=∠BEH,BD=BE,
∴△OBD≌△HEB,
∴BH=OD,EH=OB,
∵D(-2,0),B(0,4),
∴OB=4,OD=2,
∴BH=2,EH=4,
∴OH=OB+BH=6,∴E(-4,6),
∴EF=OH=6,OEH=4,
∴S四边形OBEF=![]() (OB+EF)×OF=20,
(OB+EF)×OF=20,
∵直线y=kx-4k将四边形OBEF分为面积相等的两部分,
∴S四边形OBGF=![]() S四边形OBEF=10,
S四边形OBEF=10,
∴S四边形OBFE=![]() (FG+OB×OF=
(FG+OB×OF=![]() ×(FG+4)×4=2(FG+4)=10,
×(FG+4)×4=2(FG+4)=10,
∴FG=1,∴G(-4,1)
将G(-4,1)代入直线y=kx-4k,得,1=-4k-4k,
∴k=![]() .
.
②如图1,

当DE=BD,∠BDE=90°时,
∴∠EDF+∠BDO=90°,
∴∠DEF=∠BDO,
在△DEF和△BDO中,∠DEF= ∠BOD=90°,∠DEF=∠BDO,DBD,
∴△DEF≌△BDO,
∴EF=OD=2,DF=OB=4,
∴OF=6,
∴F(-6,2)
∴S四边形OBEF=![]() (EF+OB)×OF=
(EF+OB)×OF=![]() ×(2-4)×6=18,
×(2-4)×6=18,
∵直线y=kx-4k将四边形OBEF分为面积相等的两部分,
所以直线y=kx-4k分成的两部分的面积为9,
∵直线y=kx-4k恒过A(4,0),
∴I、当直线y=kx-4k和线段EF相交,
∴S四边形OHGF=9,
∵H(0,-4k),
∴OH=-4k,
∵G点的横坐标为-6,
∴G(-6,-10k),
∴FG=-10k,
∴S四边形OHGF=![]() (-4k=10k)×6=9.
(-4k=10k)×6=9.
∴k=-![]() ,
,
II、当直线y=kx-4k①和线段EB相交,
∴S△MBN=9,
∵N(0,-4k)
∴BN=4(k+1),
∵B(0,4),E(-6,2),
∴直线BE的解析式为y=![]() x+4②
x+4②
联立①②得,点M的横坐标为![]() ,
,
∴S△MBN=![]() ×4(k+1)×
×4(k+1)×![]() =9,
=9,
∴k=![]() (舍)或k=
(舍)或k=![]() .
.
即:满足条件的k值为![]() 或-
或-![]() 或
或![]() .
.
(3)过M作MN⊥x轴,垂足为N.
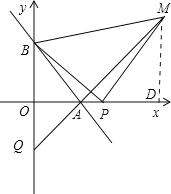
∵∠BPM=90°,∴∠BPO+MPN=90°.
∵∠AOB=∠MNP=90°,∴∠BPO=∠PMN,∠PBO=∠MPN.
∵BP=MP,∴△PBO≌△MPN,
∴ MN=OP,PN=AO=BO,
∴OP=OA+AP=PN+AP=AN,
∴MN=AN,∠MAN=45°.
∵∠BAO=45°,
∴△BAQ是等腰直角三角形.
∴OB=OQ=4.
∴无论P点怎么动,OQ的长不变.
“点睛”此题是一次函数综合题,主要考查了非负性,全等三角形的判定和性质,梯形的面积公式,三角形面积公式,等腰直角三角形的判定和性质,解题关键是求出k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,∠BAC=90°,P是△ABC内一点,PA=1,PB=3,PC=
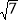 .求∠CPA的度数.
.求∠CPA的度数.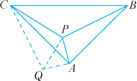
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何图形中不是中心对称图形的是( )
A. 圆 B. 平行四边形 C. 正三角形 D. 正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭,小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50 km为标准,多于50 km的记为“+”,不足50 km的记为“-”,刚好50 km的记为“0”.
第一天
第二天
第三天
第四天
第五天
第六天
第七天
路程(km)
-8
-11
-14
0
-16
+41
+8
(1)请求出这七天中平均每天行驶多少千米?
(2)若每天行驶100 km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的
 ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016浙江省温州市第23题)如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m=
 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只甲虫在5×5的方格(每小格边长为1m)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫(A,B,C,D都在格点上).规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)A→C( , ),B→C( , ),C→ (+1, );
(2)若这只甲虫沿着网格线的行走路线为A→D→C→B,请计算该甲虫走过的最短路程;
(3)若这只甲虫从A处去P处的行走路线依次为(+2,+1),(+3,+2),(﹣2,﹣1),(﹣2,﹣2),请在图中标出P的位置.
(4)在(3)中甲虫若每走1m需消耗1.5焦耳的能量,则甲虫从A走到P的过程中共需消耗多少焦耳的能量?

相关试题

