【题目】一只甲虫在5×5的方格(每小格边长为1m)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫(A,B,C,D都在格点上).规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)A→C( , ),B→C( , ),C→ (+1, );
(2)若这只甲虫沿着网格线的行走路线为A→D→C→B,请计算该甲虫走过的最短路程;
(3)若这只甲虫从A处去P处的行走路线依次为(+2,+1),(+3,+2),(﹣2,﹣1),(﹣2,﹣2),请在图中标出P的位置.
(4)在(3)中甲虫若每走1m需消耗1.5焦耳的能量,则甲虫从A走到P的过程中共需消耗多少焦耳的能量?

参考答案:
【答案】(1)见解析;(2)该甲虫走过的最短路程为11;(3)图形见解析;(4)甲虫从A走到P的过程中共需消耗22.5焦耳的能量.
【解析】试题分析: ![]() 根据规定:第一个数表示左右方向,第二个数表示上下方向,结合图形解答.
根据规定:第一个数表示左右方向,第二个数表示上下方向,结合图形解答.![]() 根据网格图形列式计算即可得解.
根据网格图形列式计算即可得解.![]() 根据点的坐标的规定在图形中找出所到达的位置即可得解.
根据点的坐标的规定在图形中找出所到达的位置即可得解.![]() 先根据路线求出所走过的路程,然后乘以
先根据路线求出所走过的路程,然后乘以![]() 计算即可得解.
计算即可得解.
试题解析:
![]()
![]() 该甲虫走过的最短路程为
该甲虫走过的最短路程为![]()
![]() 如图所示:
如图所示:

![]() 焦耳,
焦耳,
答:甲虫从![]() 走到
走到![]() 的过程中共需消耗
的过程中共需消耗![]() 焦耳的能量.
焦耳的能量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足
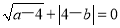
(1)求A、B两点的坐标;
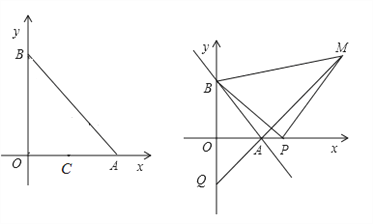
(2)C为OA的中点,作点C关于y轴的对称点D,以BD为直角边在第二象限作等腰Rt△BDE,过点E作EF⊥x轴于点F.若直线y=kx-4k将四边形OBEF分为面积相等的两部分,求k的值;
(3)如图,P为x轴上A点右侧任意一点,以BP为边作等腰Rt△PBM,其中PB=PM,直线MA交y轴于点Q,当点P在x轴上运动时,线段OQ的长是否发生变化?若不变,求其值;若变化,求线段OQ的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的
 ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
-
科目: 来源: 题型:
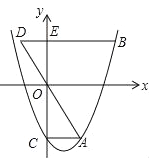
查看答案和解析>>【题目】(2016浙江省温州市第23题)如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m=
 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】各分母系数(都是整数)的最小公倍数与所有字母的的积叫做最简公分母,它类似于小学分数中的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四组数据中,能构成三角形的边长的是( )
A.1,2,3B.2,3,6C.6,8,10D.7,3,3
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据分式的基本性质,把几个异分母的分式分别化成与原来的分式的同分母的分式,叫做分式的通分.
相关试题

