【题目】老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
![]() +(﹣3x2+5x﹣7)=﹣2x2+3x﹣6
+(﹣3x2+5x﹣7)=﹣2x2+3x﹣6
(1)求所捂的多项式;
(2)若x是![]() x=﹣
x=﹣![]() x+3的解,求所捂多项式的值;
x+3的解,求所捂多项式的值;
(3)若x为正整数,任取x几个值并求出所捂多项式的值,你能发现什么规律?
(4)若所捂多项式的值为144,请直接写出x的取值.
参考答案:
【答案】(1)x2﹣2x+1;(2)若x是![]() x=﹣
x=﹣![]() x+3的解,所捂多项式的值是9;(3)所捂多项式的值是代入的正整数x﹣1的平方;(4)x的值是13.
x+3的解,所捂多项式的值是9;(3)所捂多项式的值是代入的正整数x﹣1的平方;(4)x的值是13.
【解析】
试题分析:(1)根据题意列出整式相加减的式子,再去括号,合并同类项即可;
(2)先求出![]() x=﹣
x=﹣![]() x+3的解,然后代入(1)中求得的所捂的多项式即可;
x+3的解,然后代入(1)中求得的所捂的多项式即可;
(3)令x=1,2,3求出所捂多项式的值,找出规律即可;
(4)根据第(3)问发现的规律可以直接写出x的值.
解:(1)(﹣2x2+3x﹣6)﹣(﹣3x2+5x﹣7)
=﹣2x2+3x﹣6+3x2﹣5x+7
=x2﹣2x+1,
即所捂的多项式是x2﹣2x+1;
(2)∵x是![]() x=﹣
x=﹣![]() x+3的解,
x+3的解,
∴x=4,
∴x2﹣2x+1=42﹣2×4+1=9,
即若x是![]() x=﹣
x=﹣![]() x+3的解,所捂多项式的值是9;
x+3的解,所捂多项式的值是9;
(3)当x=1时,x2﹣2x+1=1﹣2+1=0;
当x=2时,x2﹣2x+1=4﹣4+1=1;
当x=3时,x2﹣2x+1=9﹣6+1=4;
当x=4时,x2﹣2x+1=16﹣8+1=9,
由上可以发现规律是所捂多项式的值是代入的正整数x﹣1的平方;
(4)若所捂多项式的值为144,x的取值是13.
∵144=122,
∴x的值是13.
-
科目: 来源: 题型:
查看答案和解析>>【题目】O为直线DA上一点,OB⊥OF,EO是∠AOB的平分线.
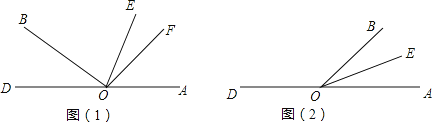
(1)如图(1),若∠AOB=130°,求∠EOF的度数;
(2)若∠AOB=α,90°<α<180°,求∠EOF的度数;
(3)若∠AOB=α,0°<α<90°,请在图(2)中画出射线OF,使得(2)中∠EOF的结果仍然成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个角的补角是这个角的余角的3倍,则这个角的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+6分别交x轴、y轴于A、B两点,抛物线y=﹣
x+6分别交x轴、y轴于A、B两点,抛物线y=﹣ x2+8,与y轴交于点D,点P是抛物线在第一象限部分上的一动点,过点P作PC⊥x轴于点C.
x2+8,与y轴交于点D,点P是抛物线在第一象限部分上的一动点,过点P作PC⊥x轴于点C.
(1)点A的坐标为 ,点D的坐标为 ;
(2)探究发现:
①假设P与点D重合,则PB+PC= ;(直接填写答案)
②试判断:对于任意一点P,PB+PC的值是否为定值?并说明理由;
(3)试判断△PAB的面积是否存在最大值?若存在,求出最大值,并求出此时点P的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=﹣
 x+4的图象与x轴交于A,与y轴交于点B.
x+4的图象与x轴交于A,与y轴交于点B.
(1)求点A,B的坐标并在如图的坐标系中画出函数y=﹣
 x+4的图象;
x+4的图象;(2)若一次函数y=kx﹣2的图象经过点A,求它的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:
①(﹣11)+5
②5﹣(﹣
 )+(﹣7)﹣
)+(﹣7)﹣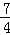
③(﹣3)2+(﹣16)÷[(﹣
 )÷(﹣
)÷(﹣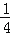 )]
)](2)化简并求值
3(x2y+xy2)﹣2(xy+xy2)﹣
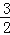 x2y,其中x是绝对值等于2的负数,y是最大的负整数.
x2y,其中x是绝对值等于2的负数,y是最大的负整数. -
科目: 来源: 题型:
查看答案和解析>>【题目】居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A 非常赞同;B 赞同但要有时间限制;C 无所谓;D 不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.
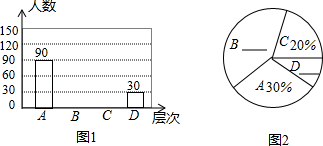
请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
相关试题

