【题目】如图1,在正方形ABCD中,点E,F分别是边AB,BC上的点,且BE=CF.连结CE,DF.将线段FD绕点F逆时针旋转90°,得到线段FG.
(1)依题意将图1补全;
(2)连结EG,请判断:EG与CF的数量关系是 ,位置关系是 ;并证明你的结论;
(3)当FG经过BE中点时,写出求∠CDF度数的思路.

参考答案:
【答案】(1)见解析(2)EG与CF的数量关系是:EG=CF,位置关系是:EG∥CF;(3)当FG经过BE中点P时
【解析】分析:(1)根据要求画出图形即可;
(2)只要证明四边形EGFC是平行四边形即可;
(3)首先证明![]() ,求出
,求出![]() 即可解决问题.
即可解决问题.
详解:(1)如图所示:
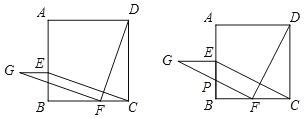 ;
;
(2)EG与CF的数量关系是:EG=CF,位置关系是:EG∥CF;
证明:∵正方形ABCD,
∴BC=CD,![]()
∵BE=CF,
∴△BCE≌△CDF
∴DF=CE,∠BEC=∠CFD.
∵![]()
∴![]()
即CE⊥DF,
∵线段FD绕点F逆时针旋转![]() ,得到线段FG,
,得到线段FG,
∴CE∥FG,DF=FG.
∴CE=FG.
∴四边形GFCE是平行四边形。
∴EG=CF,EG∥CF;
故答案为EG=CF,EG∥CF.
(3)当FG经过BE中点P时,
由△BCE≌△CDF,可得∠CDF=∠BCE.
由![]() ,可得∠BCE=∠G.
,可得∠BCE=∠G.
即∠CDF═∠G,
由BE=CF=GE,可得![]()
利用锐角三角函数,可求∠G的度数,从而可求∠CDF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A顺时针旋转60°得到△ADE,点C的对应点E恰好落在BA的延长线上,DE与BC交于点F,连接BD.下列结论不一定正确的是( )
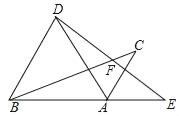
A. AD=BD B. AC∥BD C. DF=EF D. ∠CBD=∠E
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农户承包荒山若干亩,今年水果总产量为18000 千克,此水果在市场上每千克售 a 元,在果园每千克售b 元( b a ),该农户将水果拉到市场出售平均每天出售1000 千克,需8 人帮忙,每人每天付工资 25 元,农用车运费及其他各项税费平均每天100 元.
(1)分别用 a,b 表示两种方式出售水果的收入;
(2)若 a1.3元, b1.1元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣4mx+4m+4(m≠0)的顶点为P.P,M两点关于原点O成中心对称.
(1)求点P,M的坐标;
(2)若该抛物线经过原点,求抛物线的表达式;
(3)在(2)的条件下,将抛物线沿x轴翻折,翻折后的图象在0≤x≤5的部分记为图象H,点N为抛物线对称轴上的一个动点,经过M,N的直线与图象H有两个公共点,结合图象求出点N的纵坐标n的取值范围.
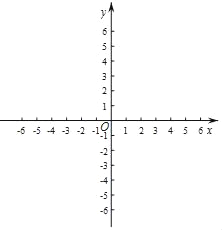
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解七年级学生的身体素质情况,体育老师对该年级部分学生进行了一分钟跳绳次数的测试,并把测试成绩绘制成如图所示的频数表和频数直方图(每组含前一个边界值,不含后一个边界值).


(1)参加测试的学生有多少人?
(2)求
 ,
, 的值,并把频数直方图补充完整.
的值,并把频数直方图补充完整.(3)若该年级共有
 名学生,估计该年级学生一分钟跳绳次数不少于
名学生,估计该年级学生一分钟跳绳次数不少于 次的人数.
次的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两支“徒步队”到野外沿相同路线徒步,徒步的路程为24千米.甲队步行速度为4千米/时,乙队步行速度为6千米/时.甲队出发1小时后,乙队才出发,同时乙队派一名联络员跑步在两队之间来回进行一次联络(不停顿),他跑步的速度为10千米/时.
(1)乙队追上甲队需要多长时间?
(2)联络员从出发到与甲队联系上后返回乙队时,他跑步的总路程是多少?
(3)从甲队出发开始到乙队完成徒步路程时止,何时两队间间隔的路程为1千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点 O 为直线 AB 上一点,过点 O 作射线 OC,使∠BOC=135°,将一个含 45°角的直角三角尺的一个顶点放在点 O 处,斜边 OM 与直线 AB 重合,另外两条直角边都在直线 AB 的下方.
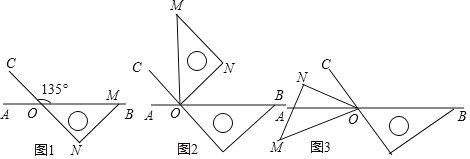
(1)将图 1 中的三角尺绕着点 O 逆时针旋转 90°,如图 2 所示,此时∠BOM= 度(答案直接填写在答题卡的横线上);在图 2 中,OM 是否平分∠CON ? 请说明理由;
(2)紧接着将图 2 中的三角板绕点 O 逆时针继续旋转到图 3 的位置所示,使得 ON 在∠AOC 的内部,请探究:∠AOM 与∠CON 之间的数量关系,并说明理由;
(3)将图 1 中的三角板绕点 O 按每秒 5°的速度沿逆时针方向旋转一周,在旋转的过程中, 第 t 秒时,直线 ON 恰好平分锐角∠AOC,请你直接写出t 的值为多少.
相关试题

