搜索
【题目】如图，在四边形ABCD中，AD//BC ， AB=10，BC=6，AC=AD=8．
（1）求∠ACB的度数；
（2）求CD边的长.
参考答案：
【答案】
（1）
解：如图2．
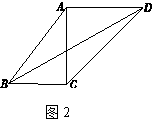
∵ △ABC中，AB=10，BC=6，AC =8，
∴ 
.
∴ △ABC是直角三角形， 
（2）
解：∵ AD//BC，
∴ 
.
∵ 在Rt△ACD中， 
，AC=AD=8，
∴ 
【解析】（1） △ABC中，由已知条件根据勾股定理逆定理得出AC2+BC2=AB2 ;从而得到 ∠ACB=90°.
（2）由 AD//BC，得到∠CAD=∠ACB=90° ；在Rt△ACD中，再根据勾股定理得到 CD2=AC2+AD2 ， 从而求出CD的长度.
【考点精析】关于本题考查的平行线的性质和勾股定理的概念，需要了解两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，动点A(a,0)在x轴的正半轴上，定点B(m, n)在第一象限内（m＜2≤a）.在△OAB外作正方形ABCD和正方形OBEF ， 连接FD ， 点M为线段FD的中点.作BB1⊥x轴于点B1 ， 作FF1⊥x轴于点F1.
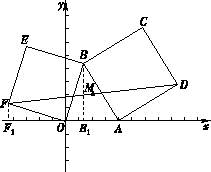
（1）填空：由△≌△ ， 及B(m, n)可得点F的坐标为 ， 同理可得点D的坐标为；（说明：点F ， 点D的坐标用含m ， n ， a的式子表示）
（2）直接利用（1）的结论解决下列问题：
①当点A在x轴的正半轴上指定范围内运动时，点M总落在一个函数图象上，求该函数的解析式（不必写出自变量x的取值范围）；
②当点A在x轴的正半轴上运动且满足2≤a≤8时，求点M所经过的路径的长. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知x＝1是关于x的一元二次方程x2+3x﹣m＝0的一个根，求m的值和方程的另一个根．
-
科目： 来源： 题型：
查看答案和解析>>【题目】利用勾股定理可以在数轴上画出表示
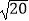的点，请依据以下思路完成画图，并保留画图痕迹：
（1）第一步：（计算）尝试满足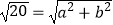
，使其中a ， b都为正整数.你取的正整数a= ， b=；
（2）第二步：（画长为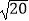 的线段）以第一步中你所取的正整数a ， b为两条直角边长画Rt△OEF ， 使O为原点，点E落在数轴的正半轴上， 
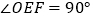，则斜边OF的长即为 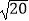.请在下面的数轴上画图：（第二步不要求尺规作图，不要求写画法）
（3）第三步：（画表示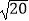 的点）在下面的数轴上画出表示 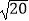的点M ， 并描述第三步的画图步骤： -
科目： 来源： 题型：
查看答案和解析>>【题目】将抛物线y＝x2+2x+5沿y轴向下平移m（m＞0）个单位，使平移后的抛物线的顶点恰好落在x轴上，求m的值及平移后抛物线的解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y1=-x2+4x和直线y2=2x．我们约定：当x任取一值时，x对应的函数值分别为y1、y2，若y1=y2，记M=y1=y2，下列判断：①当x＞2时，M=y2；②当x＜0时，x值越大，M值越大；③使得M大于4的x值不存在；④若M=2，则x=1．其中正确的有（ ）
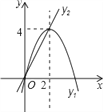
A. ③④ B. ②③ C. ②④ D. ①④
-
科目： 来源： 题型：
查看答案和解析>>【题目】“十一”黄金周期间，淮安动物园在7天假期中每天接待的人数变化如下表(正数表示比前一天多的人数，负数表示比前一天少的人数)，把9月30日的游客人数记为a万人．
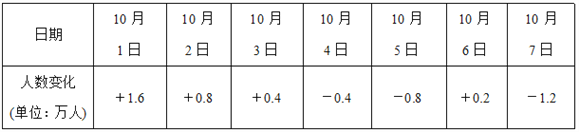
(1)请用含a的代数式表示10月2日的游客人数；
(2)请判断七天内游客人数最多的是哪天，有多少人？
(3)若9月30日的游客人数为2万人，门票每人10元，问黄金周期间淮安动物园门票收入是多少元？
相关试题
