【题目】阅读下列材料,然后解答后面的问题. 我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得 ![]() ,(x、y为正整数)∴
,(x、y为正整数)∴ ![]() 则有0<x<6.又
则有0<x<6.又 ![]() 为正整数,则
为正整数,则 ![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入 ![]() .
.
∴2x+3y=12的正整数解为 ![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解:
(2)若 ![]() 为自然数,则满足条件的x值有个;
为自然数,则满足条件的x值有个;
A.2
B.3
C.4
D.5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
参考答案:
【答案】
(1)解:由2x+y=5,得y=5﹣2x(x、y为正整数).
所以 ![]() ,即0<x<
,即0<x< ![]()
∴当x=1时,y=3;
当x=2时,y=1.
即方程的正整数解是 ![]() 或
或 ![]() .(只要写出其中的一组即可)
.(只要写出其中的一组即可)
(2)C
(3)解:设购买单价为3元的笔记本m本,单价为5元的钢笔n支.
则根据题意得:3m+5n=35,其中m、n均为自然数.
于是有: ![]() ,
,
解得: 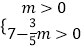 ,
,
所以0<m< ![]() .
.
由于n=7﹣ ![]() m为正整数,则
m为正整数,则 ![]() 为正整数,可知m为5的倍数.
为正整数,可知m为5的倍数.
∴当m=5时,n=4;
当m=10时,n=1.
答:有两种购买方案:即购买单价为3元的笔记本5本,单价为5元的钢笔4支;
或购买单价为3元的笔记本10本,单价为5元的钢笔1支.
【解析】(2)同样,若 ![]() 为自然数, 则有:0<x﹣2≤6,即2<x≤8.
为自然数, 则有:0<x﹣2≤6,即2<x≤8.
当x=3时, ![]() ;
;
当x=4时, ![]() ;
;
当x=5时, ![]() ;
;
当x=8时, ![]() .
.
即满足条件x的值有4个,
故选C.
-
科目: 来源: 题型:
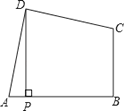
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD , DP⊥AB于P . 若四边形ABCD的面积是18,则DP的长是( ).
A.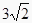
B.2
C.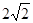
D.18 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示)
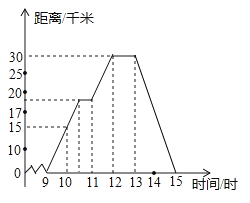
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:
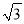 ,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留一位小数,
,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留一位小数, 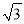 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】邻补角的两条平分线互相_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】证明:(ac-bd)2+(bc+ad)2=(a2+b2)(c2+d2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程x2﹣2x+k=0有两个相等实根,则k=_____.
相关试题

