【题目】如图,已知直线y=﹣x﹣(k+1)与双曲线y= ![]() 相交于B、C两点,与x轴相交于A点,BM⊥x轴交x轴于点M,S△OMB=
相交于B、C两点,与x轴相交于A点,BM⊥x轴交x轴于点M,S△OMB= ![]()
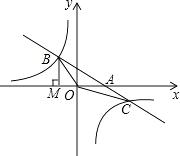
(1)求这两个函数的解析式;
(2)若已知点C的横坐标为3,求A、C两点坐标;
(3)在(2)条件下,是否存在点P,使以A、O、C、P为顶点的四边形是平行四边形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵S△OMB= ![]() =
= ![]() ×OM×BM=
×OM×BM= ![]() |k|,由反比例函数图象在第二、四象限,
|k|,由反比例函数图象在第二、四象限,
∴k=﹣3,
∴这两个函数的解析式分别为:y=﹣ ![]() ,y=﹣x+2
,y=﹣x+2
(2)
解:在y=﹣x+2中,
设y=0,则x=2,
所以A(2,0),
将x=3代入y=﹣ ![]() 得,y=﹣1,
得,y=﹣1,
所以C(3,﹣1)
(3)
解:当AO是对角线时,由C点坐标(3,﹣1),可得:点P1(﹣1,1);
当OC是对角线时,AO=P2C=2,则点P2(1,﹣1);
当AC是对角线时,AO=CP3,则点P3(5,﹣1);
故存在P(﹣1,1)或(1,﹣1)或(5,﹣1),使以A、O、C、P为顶点的四边形为平行四边形.
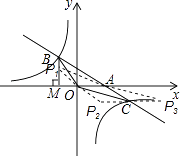
【解析】(1)利用S△OMB= ![]() ,结合反比例函数图象的性质得出k的值,进而得出答案;(2)利用图象上点的坐标性质分别求出A,C点坐标;(3)以两边为邻边,另一边为对角线画平行四边形是可行的,所以点P存在.
,结合反比例函数图象的性质得出k的值,进而得出答案;(2)利用图象上点的坐标性质分别求出A,C点坐标;(3)以两边为邻边,另一边为对角线画平行四边形是可行的,所以点P存在.
【考点精析】解答此题的关键在于理解一次函数的概念的相关知识,掌握一般地,如果y=kx+b(k,b是常数,k不等于0),那么y叫做x的一次函数,以及对反比例函数的概念的理解,了解形如y=k/x(k为常数,k≠0)的函数称为反比例函数.自变量x的取值范围是x不等于0的一切实数,函数的取值范围也是一切非零实数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮从一本书的第m页开始读,一直读到第n页,则他一共读了( )
A. (m+n)页 B. (n-m)页 C. (n-m-1)页 D. (n-m+1)页
-
科目: 来源: 题型:
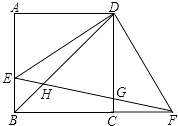
查看答案和解析>>【题目】如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(﹣3,﹣2)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】农民张大伯因病住院,手术费为a元,其它费用为b元.由于参加农村合作医疗,
手术费报销85%,其它费用报销60%,则张大伯此次住院可报销 ▲ 元.(用代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】16的平方根是( )
A.2
B.4
C.﹣2或2
D.﹣4或4 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=3(x﹣1)2+2的最小值是( )
A.2B.1C.﹣1D.﹣2
相关试题

