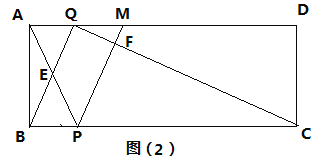
【题目】如图(1),矩形ABCD,AB=2cm,AD=6cm,P、Q分别为两个动点,点P从B出发沿边BC运动,每秒1cm,点Q从B出发沿边B—C—D运动,每秒2cm.
(1)若P、Q两点同时出发,其中一点到达终点时另一点也随之停止,设△BPQ面积为S,时间为t秒,求S关于t的函数关系式及自变量的取值范围;

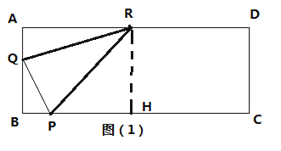
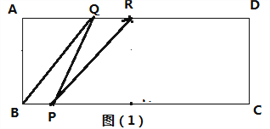
(2)若R为AD中点,连接RP、RQ,当以R、P、Q为顶点的三角形与△BPQ相似(含全等)时,求t的值;
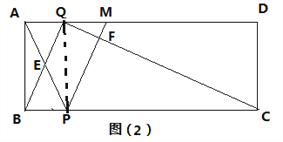
(3)如图(2)M为AD边上一点,AM=2,点Q在1.5秒时便停止运动,点P继续在BC上运动,AP与BQ交于点E,PM交CQ于点F,设四边形QEPF的面积为y,求y的最大值.
参考答案:
【答案】(1)![]() ,
, ![]() ;(2)t=0.25或
;(2)t=0.25或![]() ;(3)
;(3)![]()
【解析】(1)根据矩形的对边相等表示出BC,然后表示出PB、QB,再根据三角形的面积列式整理即可得解,根据点Q先到达终点确定出x的取值范围即可;
(2)进行分类讨论求解即可;
(3)根据面积计算得出函数关系式,再求出最大值 即可.
试题解析:(1) ![]()
![]()
(2)当∠RQP=90时,△ARQ∽△BQP, ![]() ,AQ=1.5,BQ=0.5,t=0.25
,AQ=1.5,BQ=0.5,t=0.25
当∠QPR=90时,△HPR∽△BQP, ![]() ,PH=4 不成立
,PH=4 不成立
当Q在AR上时,若QR=BP,则△RPQ全等于△BQP, ![]() ,
, ![]()
(3)连接PQ,则BP=t,则PC=6﹣x,
∵AM∥DP,
∴![]() ,
,
∴![]()
∵S△APQ=![]() ABAQ=t,
ABAQ=t,
∴S△abe=![]() ,
,
同理可得,S△PQF=![]() ,
,
∴y=![]() +
+![]() =
=![]()
![]()
当t=3时,上式等号成立,
∴y的最大值为: ![]() .
.
-
科目: 来源: 题型:
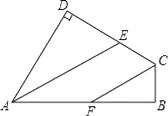
查看答案和解析>>【题目】如图在四边形ABCD中,∠B=∠D=90°,AE、CF分别平分∠BAD和∠BCD.试问直线AE、CF的位置关系如何?请说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b互为相反数,c是最大的负整数,d是最小的正整数. 求(a+b)d+d﹣c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一点到某圆的最小距离为4,最大距离为9,则该圆的半径是( )
A.2.5或6.5B.2.5C.6.5D.5或13
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD的边长为5,E在BC边上运动,DE的中点G,EG绕E顺时针旋转90°得EF,问CE为多少时A、C、F在一条直线上 ( )

A.
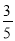 B.
B. 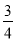 C.
C. 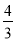 D.
D. 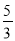
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知﹣5x2m﹣1yn与11xn+2y﹣4﹣3m的积与x7y是同类项,试求出2n﹣m﹣9的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A是第一象限内横坐标为
 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是______.
的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是______.
相关试题

