【题目】已知,点M是二次函数y=ax2(a>0)图象上的一点,点F的坐标为(0,![]() ),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为
),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为![]() .
.
(1)求a的值;
(2)当O,Q,M三点在同一条直线上时,求点M和点Q的坐标;
(3)当点M在第一象限时,过点M作MN⊥x轴,垂足为点N,求证:MF=MN+OF.

参考答案:
【答案】(1)y=x2;(2)M1(![]() ,
,![]() ),Q1(
),Q1(![]() ,
,![]() ),M2(﹣
),M2(﹣![]() ,
,![]() ),Q2(﹣
),Q2(﹣![]() ,
,![]() );(3)详见解析.
);(3)详见解析.
【解析】
试题分析:(1)设Q(m,![]() ),F(0,
),F(0,![]() ),由QO=QF,根据勾股定理列出方程即可求得a值;(2)设M(t,t2),Q(m,
),由QO=QF,根据勾股定理列出方程即可求得a值;(2)设M(t,t2),Q(m,![]() ),根据KOM=KOQ,求出t、m的关系,根据QO=QM列出方程即可解决问题.(3)设M(n,n2)(n>0),则N(n,0),F(0,
),根据KOM=KOQ,求出t、m的关系,根据QO=QM列出方程即可解决问题.(3)设M(n,n2)(n>0),则N(n,0),F(0,![]() ),利用勾股定理求出MF即可解决问题.
),利用勾股定理求出MF即可解决问题.
试题解析:(1)∵圆心O的纵坐标为![]() ,
,
∴设Q(m,![]() ),F(0,
),F(0,![]() ),
),
∵QO=QF,
∴m2+(![]() )2=m2+(
)2=m2+(![]() ﹣
﹣![]() )2,
)2,
∴a=1,
∴抛物线为y=x2.
(2)∵M在抛物线上,设M(t,t2),Q(m,![]() ),
),
∵O、Q、M在同一直线上,
∴KOM=KOQ,
∴![]() =
=![]() ,
,
∴m=![]() ,
,
∵QO=QM,
∴m2+(![]() )2=(m﹣t)2=(
)2=(m﹣t)2=(![]() ﹣t2)2,
﹣t2)2,
整理得到:﹣![]() t2+t4+t2﹣2mt=0,
t2+t4+t2﹣2mt=0,
∴4t4+3t2﹣1=0,
∴(t2+1)(4t2﹣1)=0,
∴t1=![]() ,t2=﹣
,t2=﹣![]() ,
,
当t1=![]() 时,m1=
时,m1=![]() ,
,
当t2=﹣![]() 时,m2=﹣
时,m2=﹣![]() .
.
∴M1(![]() ,
,![]() ),Q1(
),Q1(![]() ,
,![]() ),M2(﹣
),M2(﹣![]() ,
,![]() ),Q2(﹣
),Q2(﹣![]() ,
,![]() ).
).
(3)设M(n,n2)(n>0),
∴N(n,0),F(0,![]() ),
),
∴MF=![]() =
=![]() =n2+
=n2+![]() ,MN+OF=n2+
,MN+OF=n2+![]() ,
,
∴MF=MN+OF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣3xy2z3的系数和次数分别是( )
A. ﹣3,5 B. ﹣3,8 C. ﹣3,7 D. ﹣3,6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣3,0)、B(5,0)、C(0,5)三点,O为坐标原点
(1)求此抛物线的解析式;
(2)若把抛物线y=ax2+bx+c(a≠0)向下平移
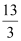 个单位长度,再向右平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
个单位长度,再向右平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;(3)设点P在y轴上,且满足∠OPA+∠OCA=∠CBA,求CP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.在一个三角形中,至多有两个内角是钝角
B.三角形的两边之和小于第三边
C.在一个三角形中,至多有两个内角是锐角
D.在同一平面内,垂直于同一直线的两直线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】长城总长约为6700010米,用科学记数法表示是(保留两个有效数字)
A、6.7×105米 B、6.7×106米 C、6.7×107米 D、6.7×108米
-
科目: 来源: 题型:
查看答案和解析>>【题目】在以下几何体中,三视图完全相同的是( )
A. 圆锥 B. 正方体 C. 圆柱 D. 五棱柱
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知xm=3,xn=4,则xm+2n= .
相关试题

