【题目】如图,在平面直角坐标系中,点A(20,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.
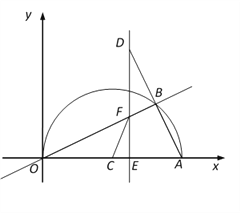
(1)当∠AOB=30°时,求弧OB的长度;
(2)当DE=16时,求线段EF的长;
(3)在点B运动过程中,是否存在以点E、C、F为顶点的三角形与△AOB相似,若存在,请求出此
时点E的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)6或24;(3)E点为
;(2)6或24;(3)E点为![]()
【解析】试题分析: (1)连接BC,由已知得∠ACB=2∠AOB=60°,AC=![]() AO=10,根据弧长公式求解;
AO=10,根据弧长公式求解;
(2)连接OD,由垂直平分线的性质得OD=OA=20,又DE=16,在Rt△ODE中,由勾股定理求OE,依题意证明△OEF∽△DEA,利用相似比求EF;
(3)存在.当以点E、C、F为顶点的三角形与△AOB相似时,分为①当交点E在O,C之间时,由以点E、C、F为顶点的三角形与△AOB相似,有∠ECF=∠BOA或∠ECF=∠OAB,②当交点E在点C的右侧时,要使△ECF与△BAO相似,只能使∠ECF=∠BAO,③当交点E在点O的左侧时,要使△ECF与△BAO相似,只能使∠ECF=∠BAO,三种情况,分别求E点坐标.
试题解析: (1)连接BC,
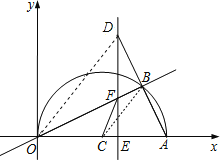
∵A(20,0),∴OA=20,CA=10,
∵∠AOB=30°,
∴∠ACB=2∠AOB=60°,
∴弧AB的长=![]() =
=![]() ;
;
(2)①若D在第一象限,
连接OD,
∵OA是⊙C直径,
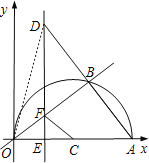
∴∠OBA=90°,
又∵AB=BD,
∴OB是AD的垂直平分线,
∴OD=OA=20,
在Rt△ODE中,
OE=![]() =
=![]() ,
,
∴AE=AOOE=2012=8,
由∠AOB=∠ADE=90°∠OAB,∠OEF=∠DEA,
得△OEF∽△DEA,
∴![]() ,即
,即![]() ,
,
∴EF=6;
②若D在第二象限,
连接OD,
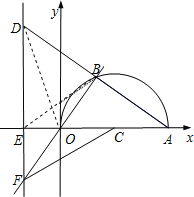
∵OA是⊙C直径,
∴∠OBA=90°,
又∵AB=BD,
∴OB是AD的垂直平分线,
∴OD=OA=10,
在Rt△ODE中,
OE=![]() =
=![]() ,
,
∴AE=AO+OE=20+12=32,
由∠AOB=∠ADE=90°∠OAB,∠OEF=∠DEA,
得△OEF∽△DEA
∴![]() ,即
,即![]() ,
,
∴EF=24;
∴EF=6或24;
(3)设OE=x,
①当交点E在O,C之间时,由以点E. C.F为顶点的三角
形与△AOB相似,有∠ECF=∠BOA或∠ECF=∠OAB,
当∠ECF=∠BOA时,此时△OCF为等腰三角形,点E为OC
中点,即OE=5,
∴E (5,0);
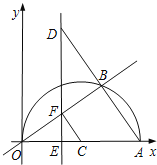
当∠ECF=∠OAB时,有CE=10x,AE=20x,
∴CF∥AB,有CF=![]() AB,
AB,
∵△ECF∽△EAD,
∴![]() ,即
,即![]() ,解得:x=
,解得:x=![]() ,
,
∴E (![]() ,0);
,0);
②当交点E在点C的右侧时,
∵∠ECF>∠BOA,
∴要使△ECF与△BAO相似,只能使∠ECF=∠BAO,
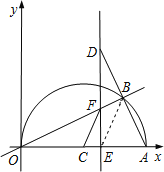
连接BE,
∵BE为Rt△ADE斜边上的中线,
∴BE=AB=BD,
∴∠BEA=∠BAO,
∴∠BEA=∠ECF,
∴CF∥BE,
∴![]() ,
,
∵∠ECF=∠BAO,∠FEC=∠DEA=90°,
∴△CEF∽△AED,
∴CFAD=CEAE,
而AD=2BE,
∴![]() ,
,
即![]() ,解得x =
,解得x =![]() ,x =
,x =![]() <0(舍去),
<0(舍去),
∴E (![]() ,0);
,0);
③当交点E在点O的左侧时,
∵∠BOA=∠EOF>∠ECF.
∴要使△ECF与△BAO相似,只能使∠ECF=∠BAO

连接BE,得BE=![]() AD=AB,∠BEA=∠BAO
AD=AB,∠BEA=∠BAO
∴∠ECF=∠BEA,
∴CF∥BE,
∴![]() ,
,
又∵∠ECF=∠BAO,∠FEC=∠DEA=90,
∴△CEF∽△AED,
∴![]() ,
,
而AD=2BE,
∴![]() ,
,
∴![]() ,
,
解得x=![]() ,x=
,x=![]() (舍去),
(舍去),
∵点E在x轴负半轴上,
∴![]() (
(![]() ,0),
,0),
综上所述:存在以点E. C.F为顶点的三角形与△AOB相似,
此时点E坐标为:E点为![]() .
.
点睛: 解答本题的关键是熟练掌握相似三角形的性质:相似三角形的对应边成比例,注意对应字母在对应位置上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(15分)解下列方程:
(1)4x-3(12-x)=6x-2(8-x);
(2)
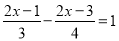 ;
;(3)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四人参加射击训练,每人各射击20次,他们射击成绩的平均数都是9.1环,各自的方差见如下表格:
甲
乙
丙
丁
方差
0.293
0.375
0.362
0.398
由上可知射击成绩最稳定的是( )
A.甲
B.乙
C.丙
D.丁 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多边形的内角和为1080°,则这个多边形是( )
A. 九边形 B. 八边形 C. 七边形 D. 六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】太阳与地球之间的平均距离约为150000000km,用科学记数法表示这一数据为( )
A.1.5×108 kmB.15×107 kmC.0.15×109 kmD.1.5×109 km
-
科目: 来源: 题型:
查看答案和解析>>【题目】)如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,E是线段AB上一点,过点E作x轴的垂线,交反比例函数图象于点F,若EF= AD,求出点E的坐标.
AD,求出点E的坐标.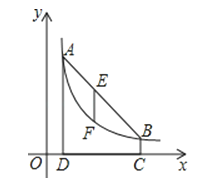
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.

(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
相关试题

