【题目】如图,点E,F在矩形的边AD,BC上,点B与点D关于直线EF对称.设点A关于直线EF的对称点为G.
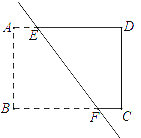
(1)画出四边形ABFE关于直线EF对称的图形;
(2)若∠FDC=16°,直接写出∠GEF的度数为 ;
(3)若BC=4,CD=3,写出求线段EF长的思路.
参考答案:
【答案】(1)见解析;(2)127°;(3)见解析.
【解析】
(1)直接利用轴对称图形的性质得出对应点位置进而得出答案;
(2)利用翻折变换的性质结合平行线的性质得出∠1度数进而得出答案;
(3)利用翻折变换的性质结合勾股定理得出答案.
(1)如图所示:
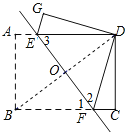
(2)∵∠FDC=16°,
∴∠DFC=74°,
由对称性得,∠1=∠2=![]()
∵AD∥BC,
∴∠AEF=∠GEF=180°-53°=127°;
故答案为:127°.
(3)思路:
a.连接BD交EF于点O.
b.在Rt△DFC中,设FC=x,则FD=4-x,由勾股定理,求得FD长;
c.Rt△BDC中,勾股可得BD=5,由点B与点D的对称性可得OD的长;
d.在Rt△DFO中,同理可求OF的长,可证EF=2OF,求得EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】慢车和快车先后从甲地出发沿直线道路匀速驶向乙地,快车比慢车晚出发0.5小时,行驶一段时间后,快车途中体息,休息后继续按原速行驶,到达乙地后停止.慢车和快车离甲地的距离y(千米)与慢车行驶时间x(小时)之间的函数关系如图所示.
(1)直接写出快车速度是 千米/小时.
(2)求快车到达乙地比慢车到达乙地早了多少小时?
(3)求线段BC对应的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A. 选举中,人们通常最关心的数据是众数
B. 从1,2,3,4,5中随机抽取一个数,取得奇数的可能性比较大
C. 甲、乙两人在相同条件下各射击10次,他们的平均成绩相同,方差分别为
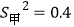 ,
,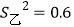 ,则甲的射击成绩较稳定
,则甲的射击成绩较稳定D. 数据3,5,4,1,-2的中位数是4
-
科目: 来源: 题型:
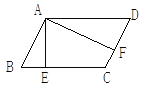
查看答案和解析>>【题目】如图,已知□ABCD中,AE⊥BC,AF⊥DC,BC∶CD= 3∶2,AB=EC,则∠EAF=( )
A.
 B.
B. 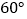 C.
C. 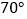 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】现在电器进入销售旺季,福清某电器超市销售每台进价分别为
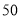 元、
元、 元的
元的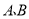 两种型号的电器,下表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入-进货成本)
两种型号的电器,下表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入-进货成本)销售时段
销售数量
销售收入
 种型号
种型号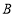 种型号
种型号第一周
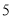 台
台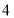 台
台 元
元第二周
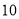 台
台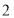 台
台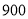 元
元(1)求
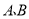 两种型号的电器销售单价;
两种型号的电器销售单价;(2)若超市准备用不超过
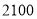 元的金额再采购这种型号的电器共
元的金额再采购这种型号的电器共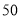 台,销售完这
台,销售完这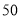 台电器实现利润超过
台电器实现利润超过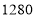 元的目标,请给出相应的采购方案;并求出利润的最大值.
元的目标,请给出相应的采购方案;并求出利润的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究与应用:

(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分面积是 (写成两数平方差的形式)
(2)小颖将阴影部分裁下来,重新拼成一个长方形,如图乙,则长方形的长是 ,宽是 ,面积是 (写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到公式 (用式子表达)
(4)运用你所得到的公式计算:10.3×9.7.
相关试题

