【题目】垫球是排球运动的一项重要技术.下列图表中的数据分别是甲、乙、内三个运动员十次垫球测试的成绩,规则为每次测试连续垫球10个,每垫球到位1个记1分.
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
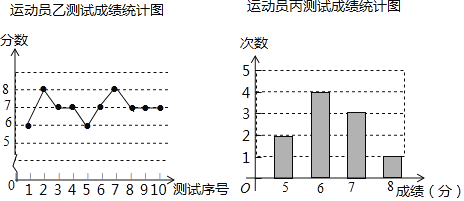
(1)写出运动员甲测试成绩的众数和中位数;
(2)试从平均数和方差两个角度综合分析,若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、s丙2=0.81)
参考答案:
【答案】(1) 甲的众数和中位数都是7分;(2) 选乙运动员更合适,理由见解析
【解析】
(1)观察表格可知甲运动员测试成绩的众数和中位数都是7分;
(2)分别求得数据的平均数,然后结合方差作出判断即可.
(1)甲运动员测试成绩中7出现的次数最多,故众数为7;
成绩排序为:5,6,7,7,7,7,7,8,8,8,
所以甲的中位数为![]() =7,
=7,
所以甲的众数和中位数都是7分.
(2)∵![]() =
=![]() (7+6+8+7+7+5+8+7+8+7)=7(分),
(7+6+8+7+7+5+8+7+8+7)=7(分),
![]() =
=![]() (6+6+7+7+7+7+7+7+8+8)=7(分),
(6+6+7+7+7+7+7+7+8+8)=7(分),
![]() =
=![]() (5×2+6×4+7×3+8×1)=6.3(分),
(5×2+6×4+7×3+8×1)=6.3(分),
∴![]() =
=![]() ,S甲2>S乙2,
,S甲2>S乙2,
∴选乙运动员更合适.
-
科目: 来源: 题型:
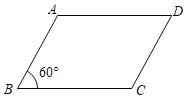
查看答案和解析>>【题目】过某矩形的两个相对的顶点作平行线,再沿着平行线剪下两个直角三角形,剩余的图形为如图所示的ABCD,AB=4,BC=6,∠ABC=60°,则原来矩形的面积是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某草莓种植大户,今年从草莓上市到销售完需要20天,售价为15元/千克,成本y(元/千克)与第x天成一次函数关系,当x=10时,y=7,当x=15时,y=6.5.
(1)求成本y(元/千克)与第x天的函数关系式并写出自变量x的取值范围;
(2)求第几天每千克的利润w(元)最大?最大利润是多少?(利润=售价-成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:
①0是最小的整数;
②有理数不是正数就是负数;
③正整数、负整数、正分数、负分数统称为有理数;
④非负数就是正数;
⑤
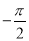 不仅是有理数,而且是分数;
不仅是有理数,而且是分数;⑥
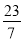 是无限不循环小数,所以不是有理数;
是无限不循环小数,所以不是有理数;⑦无限小数不都是有理数;
⑧正数中没有最小的数,负数中没有最大的数.
其中错误的说法的个数为( )
A.7个B.6个C.5个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积是( )
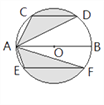
A.
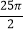 B.
B.  C.
C. 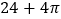 D.
D. 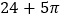
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正△ABO的边长为2,O为坐标原点,A在
 轴上,B在第二象限.△ABO沿
轴上,B在第二象限.△ABO沿  轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是________;翻滚2017次后AB中点M经过的路径长为________.
轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是________;翻滚2017次后AB中点M经过的路径长为________.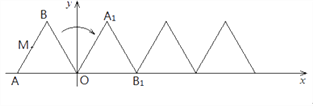
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9,
(1)求证:△COD∽△CBE;
(2)求半圆O的半径的长

相关试题

