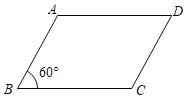
【题目】过某矩形的两个相对的顶点作平行线,再沿着平行线剪下两个直角三角形,剩余的图形为如图所示的ABCD,AB=4,BC=6,∠ABC=60°,则原来矩形的面积是__.
参考答案:
【答案】16![]() 或21
或21![]()
【解析】
分两种情况,由含30°角的直角三角形的性质求出原来矩形的长和宽,即可得出面积.
解:∵四边形ABCD是平行四边形,
∴AD=BC=6,CD=AB=4,
分两种情况:
①四边形BEDF是原来的矩形,如图1所示:

则∠E=∠EBF=90°,
∴∠ABE=90°﹣∠ABC=30°,
∴AE=![]() AB=2,BE=
AB=2,BE=![]() AE=2
AE=2![]() ,
,
∴DE=AE+AD=8,
∴矩形BEDF的面积=BE×DE=2![]() ×8=16
×8=16![]() ;
;
②四边形BGDH是原来的矩形,如图2所示:

同①得:CH=![]() BC=3,BH=
BC=3,BH=![]() CH=3
CH=3![]()
∴DH=CH+CD=7,
∴矩形BGDH的面积=BH×DH=3![]() ×7=21
×7=21![]() ;
;
综上所述,原来矩形的面积为16![]() 或21
或21![]() ;
;
故答案为:16![]() 或21
或21![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
关于x的方程:
 的解是
的解是 ,
, ;
; 即
即 的解是
的解是 ;
; 的解是
的解是 ,
, ;
; 的解是
的解是 ,
, ;
;
 请观察上述方程与解的特征,比较关于x的方程
请观察上述方程与解的特征,比较关于x的方程 与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证. 由上述的观察、比较、猜想、验证,可以得出结论:
由上述的观察、比较、猜想、验证,可以得出结论:如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这个结论解关于x的方程:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=
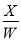 ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
-
科目: 来源: 题型:
查看答案和解析>>【题目】当
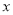 分别等于3和
分别等于3和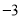 时,多项式
时,多项式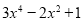 的值是( )
的值是( )A.相等B.互为倒数C.互为相反数D.异号
-
科目: 来源: 题型:
查看答案和解析>>【题目】某草莓种植大户,今年从草莓上市到销售完需要20天,售价为15元/千克,成本y(元/千克)与第x天成一次函数关系,当x=10时,y=7,当x=15时,y=6.5.
(1)求成本y(元/千克)与第x天的函数关系式并写出自变量x的取值范围;
(2)求第几天每千克的利润w(元)最大?最大利润是多少?(利润=售价-成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:
①0是最小的整数;
②有理数不是正数就是负数;
③正整数、负整数、正分数、负分数统称为有理数;
④非负数就是正数;
⑤
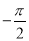 不仅是有理数,而且是分数;
不仅是有理数,而且是分数;⑥
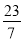 是无限不循环小数,所以不是有理数;
是无限不循环小数,所以不是有理数;⑦无限小数不都是有理数;
⑧正数中没有最小的数,负数中没有最大的数.
其中错误的说法的个数为( )
A.7个B.6个C.5个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】垫球是排球运动的一项重要技术.下列图表中的数据分别是甲、乙、内三个运动员十次垫球测试的成绩,规则为每次测试连续垫球10个,每垫球到位1个记1分.
测试序号
1
2
3
4
5
6
7
8
9
10
成绩(分)
7
6
8
7
7
5
8
7
8
7
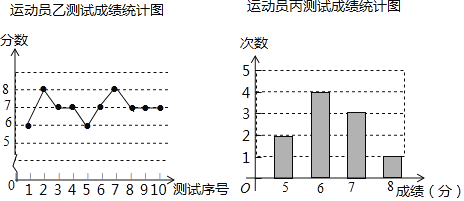
(1)写出运动员甲测试成绩的众数和中位数;
(2)试从平均数和方差两个角度综合分析,若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、s丙2=0.81)
相关试题

