【题目】如图1,在平行四边形ABCD中,对角线AC、BD交于点O,经过点O的直线AD于点E,交BC于点F.
(1)求证:OE=OF;
(2)如图2,连接AF、CE,当AF⊥FC时,在不添加辅助线的情况下,直接写出等于![]() 的线段.
的线段.

参考答案:
【答案】(1)证明见解析;(2)AO、OC、OF、OE.
【解析】
(1)结合平行四边形的性质和ASA定理证明△AOE≌△COF,从而得到OE=OF;
(2)判定四边形AFCE是矩形,然后根据平行四边形和矩形的性质求解.
解:(1)∵在平行四边形ABCD中,AD∥BC,AO=CO
∴∠CAD=∠ACB
又∵AO=CO
∴△AOE≌△COF
∴OE=OF;
(2)在在平行四边形ABCD中,![]()
由(1)可知:OE=OF,AO=CO
∴四边形AFCE是平行四边形
又∵AF⊥FC
∴∠AFC=90°
∴四边形AFCE是矩形
∴AC=EF
∴OE=OF=![]()
∴等于![]() 的线段有AO、OC、OF、OE.
的线段有AO、OC、OF、OE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知
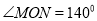 ,
, 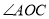 与
与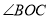 互余,
互余, 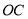 平分
平分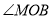 .
.(1)在图1中,若
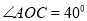 ,则
,则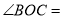 ______
______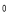 ,
,  ______
______ .
.(2)在图1中,设
 ,
,  ,请探究
,请探究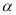 与
与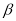 之间的数量关系(必须写出推理的主要过程,但每一步后面不必写出理由);
之间的数量关系(必须写出推理的主要过程,但每一步后面不必写出理由);(3)在已知条件不变的前提下,当
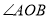 绕着点O顺时针转动到如图2的位置,此时
绕着点O顺时针转动到如图2的位置,此时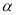 与
与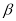 之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时
之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时 与
与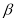 之间的数量关系.
之间的数量关系.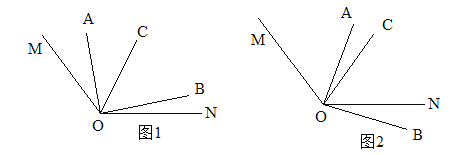
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=x+1的图象与反比例函数y=
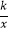 (k为常数,且k≠0)的图象都经过点A(m,2).
(k为常数,且k≠0)的图象都经过点A(m,2).
(1)求点A的坐标及反比例函数的表达式;
(2)设一次函数y=x+1的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.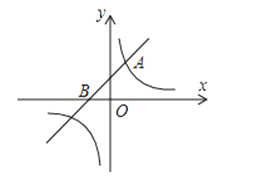
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=
 的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC=
的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC= .
.
(1)求该反比例函数和一次函数的解析式.
(2)求△BOC的面积.
(3)P是x轴上的点,且△PAC的面积与△BOC的面积相等,求P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图,说出这个图形的旋转中心,它绕旋转中心至少旋转多大角度才能与原来图形重合?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+1与y轴交于A点,与反比例函数y=
 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO= .
.
(1)求k的值;
(2)设点N(1,a)是反比例函数y= (x>0)图象上的点,在y轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在y轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点E为正方形ABCD边BC上的一点,点G为BC延长线一点,连接AE,过点E作AE⊥EF,且AE=EF,连接CF.
(1)如图1,求证:∠FCG=45°,
(2)如图2,过点D作DH//EF交AB于点H,连接HE,求证:
 ;
;(3)如图3,连接AF、DF,若AF交CD于点M,DM=2,BH=3,求DF的长.

相关试题

