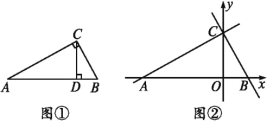
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB,
(1)图①中共有 对相似三角形,写出来分别为 (不需证明);
(2)已知AB=10,AC=8,请你求出CD的长;
(3)在(2)的情况下,如果以AB为x轴,CD为y轴,点D为坐标原点O,建立直角坐标系(如图②),若点P从点C出发,以每秒1个单位的速度沿线段CB运动,点Q从点B出发,以每秒1个单位的速度沿线段BA运动,其中一点最先到达线段的端点时,两点即刻同时停止运动;设运动时间为t秒,是否存在点P,使以点B,P,Q为顶点的三角形与△ABC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)3对,分别是:△ABC∽△ACD, △ABC∽△CBD , △ACD∽△CBD;(2)4.8;(3)存在,(1.35,3)或(3.15,1.8).
【解析】
试题(1)根据两角对应相等的两三角形相似即可得到3对相似三角形,分别为:△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD;
(2)先在△ABC中由勾股定理求出BC的长,再根据△ABC的面积不变得到![]() ABCD=
ABCD=![]() ACBC,即可求出CD的长;
ACBC,即可求出CD的长;
(3)由于∠B公共,所以以点B、P、Q为顶点的三角形与△ABC相似时,分两种情况进行讨论:①△PQB∽△ACB;②△QPB∽△ACB.
试题解析:(1)图1中共有3对相似三角形,分别为:△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD.
故答案为3,△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD;
(2)如图1,在△ABC中,∵∠ACB=90°,AB=10,AC=8,∴BC=![]() =6.
=6.
∵△ABC的面积=![]() ABCD=
ABCD=![]() ACBC,∴CD=
ACBC,∴CD=![]() =4.8;
=4.8;
(3)存在点P,使以点B、P、Q为顶点的三角形与△ABC相似,理由如下:在△BOC中,∵∠COB=90°,BC=6,OC=4.8,∴OB=![]() =3.6.
=3.6.
分两种情况:①当∠BQP=90°时,如图2①,此时△PQB∽△ACB,
∴![]() ,∴
,∴![]() ,解得t=2.25,即BQ=CP=2.25,
,解得t=2.25,即BQ=CP=2.25,
∴OQ=OB﹣BQ=3.6﹣2.25=1.35,BP=BC﹣CP=6﹣2.25=3.75.
在△BPQ中,由勾股定理,得PQ=![]() =
=![]() ,∴点P的坐标为(1.35,3);
,∴点P的坐标为(1.35,3);

②当∠BPQ=90°时,如图2②,此时△QPB∽△ACB,∴![]() ,∴
,∴![]() ,
,
解得t=3.75,即BQ=CP=3.75,BP=BC﹣CP=6﹣3.75=2.25.
过点P作PE⊥x轴于点E.
∵△QPB∽△ACB,∴![]() ,∴
,∴![]() ,∴PE=1.8.
,∴PE=1.8.
在△BPE中,BE=![]() =
=![]() ,∴OE=OB﹣BE=3.6﹣0.45=3.15,
,∴OE=OB﹣BE=3.6﹣0.45=3.15,
∴点P的坐标为(3.15,1.8);
综上可得,点P的坐标为(1.35,3)或(3.15,1.8).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.
(1)图中还有几对全等三角形,请你一一列举;
(2)求证:CF=EF.

-
科目: 来源: 题型:
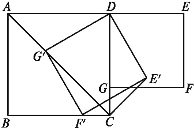
查看答案和解析>>【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE'F'G',此时点G'在AC上,连接CE',则CE'+CG'=______
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知顶点为P的抛物线C1的解析式为y=a(x-3)2(a≠0),且经过点(0,1).
(1)求a的值及抛物线C1的解析式;
(2)如图,将抛物线C1向下平移h(h>0)个单位得到抛物线C2,过点K(0,m2)(m>0)作直线l平行于x轴,与两抛物线从左到右分别相交于A,B,C,D四点,且A,C两点关于y轴对称.
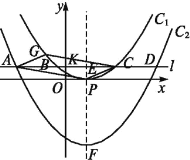
①点G在抛物线C1上,当m为何值时,四边形APCG为平行四边形?
②若抛物线C1的对称轴与直线l交于点E,与抛物线C2交于点F.试探究:在K点运动过程中,
 的值是否改变?若会,请说明理由;若不会,请求出这个值.
的值是否改变?若会,请说明理由;若不会,请求出这个值. -
科目: 来源: 题型:
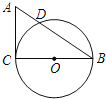
查看答案和解析>>【题目】如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问:当点E在什么位置时,直线ED与⊙O相切?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为( )
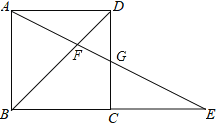
A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 抛物线
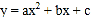 与
与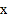 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与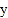 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①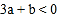 ;②
;②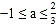 ;③对于任意实数m,
;③对于任意实数m,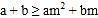 总成立;④关于
总成立;④关于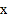 的方程
的方程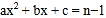 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为

A. 1 个 B. 2 个 C. 3 个 D. 4 个
相关试题

