搜索
【题目】⊙O的半径r="5" cm，圆心到直线l的距离OM="4" cm，在直线l上有一点P，且PM="3" cm，则点P（ ）
A. 在⊙O内 B. 在⊙O上
C. 在⊙O外 D. 可能在⊙O上或在⊙O内
参考答案：
【答案】B
【解析】试题分析：由条件计算出OP的长度与半径比较大小即可．
解：由题意可知△OPM为直角三角形，且PM=3，OM=4，
由勾股定理可求得OP=5=r，
故点P在⊙O上，
故选B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】操作探究：已知在纸面上有一数轴(如图所示)．
操作一：
(1)折叠纸面，使1表示的点与－1表示的点重合，则－3表示的点与________表示的点重合；
操作二：
(2)折叠纸面，使－1表示的点与3表示的点重合，回答以下问题：
①5表示的点与数________表示的点重合；
②若数轴上A、B两点之间距离为11(A在B的左侧)，且A、B两点经折叠后重合，求A、B两点表示的数是多少．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为（
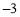，0）、（0，4），抛物线
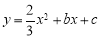经过B点，且顶点在直线
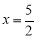上．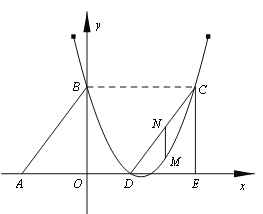
（1）求抛物线对应的函数关系式；
（2）若△DCE是由△ABO沿x轴向右平移得到的，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由；
（3）若M点是CD所在直线下方该抛物线上的一个动点，过点M作MN平行于y轴交CD于点N．设点M的横坐标为t，MN的长度为l．求l与t之间的函数关系式，并求l取最大值时，点M的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知在平行四边形ABCD中，AE⊥BC，垂足为E，CE=CD，F为CE的中点，G为CD上的一点，连接DF、EG、AG，并延长AG、BC交于点H，∠DFC=∠EGC．
（1）若CF=2，AE=3，求BE的长；
（2）求证：点G为CD中点；
（3）求证：∠AGE=2∠CEG．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把方程x（x﹣1）=0化为一般形式是______________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】数据6，5，7，7，9的众数是_____________
-
科目： 来源： 题型：
查看答案和解析>>【题目】直角三角形ABC的两条直角边是6和8，则它的外接圆的半径的长为__________．
相关试题
