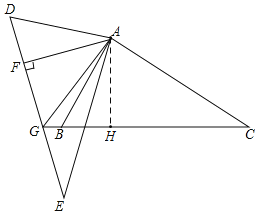
【题目】如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG,若S四边形DGBA=6,AF=![]() ,则FG的长是_____.
,则FG的长是_____.

参考答案:
【答案】4.
【解析】
过点A作AH⊥BC于H,可证明△ABC≌△ADE,得出AF=AH,再判定Rt△AFG≌Rt△AHG,即可得出![]() ,再判定Rt△ADF≌Rt△ABH,得出S四边形DGBA=S四边形AFGH=6,最后根据Rt△AFG的面积=3,进而得出FG的长.
,再判定Rt△ADF≌Rt△ABH,得出S四边形DGBA=S四边形AFGH=6,最后根据Rt△AFG的面积=3,进而得出FG的长.
解:过点A作AH⊥BC于H,如图所示:
在△ABC与△AED中,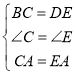 ,
,
∴△ABC≌△ADE(SAS),
∴AD=AB,S△ABC=S△AED,
又∵AF⊥DE,
即![]() ×DE×AF=
×DE×AF=![]() ×BC×AH,
×BC×AH,
∴AF=AH,
又∵AF⊥DE,AH⊥BC,
∴在Rt△AFG和Rt△AHG中,![]() ,
,
∴Rt△AFG≌Rt△AHG(HL),
同理:Rt△ADF≌Rt△ABH(HL),
∴S四边形DGBA=S四边形AFGH=6,
∵Rt△AFG≌Rt△AHG,
∴Rt△AFG的面积=3,
∵AF=![]() ,
,
∴![]() ×FG×
×FG×![]() =3,
=3,
解得:FG=4;
故答案为:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE= ;
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】据路透社报道,中国华为技术有限公司推出新的服务器芯片组,此举正值中国努力提高芯片制造能力,并减少对进口芯片的严重依赖.华为表示,其最新的7纳米64核中央处理器(CPU)将为数据中心提供更高的计算性能并降低功耗.我们知道,1纳米=0.000 000 001米,那么7纳米用科学记数法应记为( )
A.0.7×10
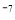 米B.7×10
米B.7×10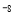 米C.7×10
米C.7×10 米D.7×10
米D.7×10 米
米 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列推理所注理由正确的是( )
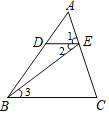
A.∵DE∥BC,∴∠1=∠C(同位角相等,两直线平行)
B.∵∠2=∠3,∴DE∥BC(两直线平行,内错角相等)
C.∵DE∥BC,∴∠2=∠3(两直线平行,内错角相等)
D.∵∠DEC+∠C=180°,∴DE∥BC(同旁内角相等,两直线平行)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:关于x的二次函数
 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子里装有3个黑球和若干白球,它们除颜色外都相同.在不允许将球倒出来数的前提下,小明为估计其中白球数,采用如下办法:随机从中摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,记下颜色,…不断重复上述过程.小明共摸100次,其中20次摸到黑球.根据上述数据,小明估计口袋中白球大约有( )
A. 10个 B. 12 个 C. 15 个 D. 18个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形
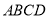 和四边形
和四边形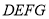 为正方形,点
为正方形,点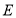 在线段
在线段 上,点
上,点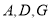 在同一直线上,连接
在同一直线上,连接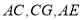 ,并延长
,并延长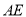 交
交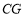 于点
于点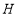 .
.(1)求证:
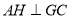 .
.(2)若
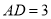 ,
,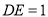 ,求线段
,求线段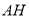 的长.
的长.(3)设
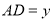 ,
,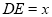 ,当点H是线段GC的中点时,则
,当点H是线段GC的中点时,则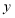 与
与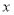 满足什么样的关系式.
满足什么样的关系式. 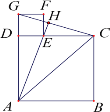
相关试题

