【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
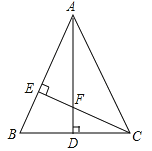
(1)△AEF≌△CEB;
(2)AF=2CD.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)由AD⊥BC,CE⊥AB,易得∠AFE=∠B,利用全等三角形的判定得△AEF≌△CEB;
(2)由全等三角形的性质得AF=BC,由等腰三角形的性质“三线合一”得BC=2CD,等量代换得出结论.
试题解析:(1)∵AD⊥BC,CE⊥AB,
∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,
∵∠CFD=∠AFE,
∴∠AFE=∠B
在△AEF与△CEB中,
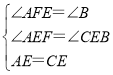
∴△AEF≌△CEB(AAS);
(2)∵AB=AC,AD⊥BC,
∴BC=2CD,
∵△AEF≌△CEB,
∴AF=BC,
∴AF=2CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°
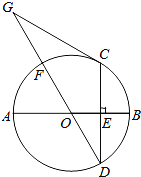
(1)求证:
 =
= .
.(2)若CD=6,求GF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+3x+m﹣1=0的两个实数根分别为x1,x2.
(1)求m的取值范围;
(2)若2(x1+x2)+x1x2+10=0,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )
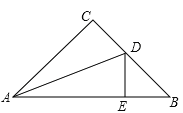
A.4cm B.6cm C.8cm D.10cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察等式:①0×2+1=1,(2)1×3+1=4,③2×4+1=9,④3×5+1=16,…,则第n个式子为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>2a,那么对于a的判断正确的是( )
A. 是正数 B. 是负数 C. 是非正数 D. 是非负数
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 3a-a=2 B. a·a2=a3 C. a6÷a3=a2 D. (a3)2=a5
相关试题

