【题目】如图,⊙O是以原点为圆心,![]() 为半径的圆,点P是直线y=﹣x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为______.
为半径的圆,点P是直线y=﹣x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为______.

参考答案:
【答案】4
【解析】试题分析:由P在直线y=-x+6上,设P(m,6-m),连接OQ,OP,由PQ为圆O的切线,得到PQ⊥OQ,在直角三角形OPQ中,利勾股定理列出关系式,配方后利用二次函数的性质即可求出PQ的最小值.
解:∵P在直线y=x+6上,
∴设P坐标为(m,6m),
连接OQ,OP,由PQ为圆O的切线,得到PQ⊥OQ,

在Rt△OPQ中,根据勾股定理得:OP2=PQ2+OQ2,
∴PQ2=m2+(6m)22=2m212m+34=2(m3)2+16,
则当m=3时,切线长PQ的最小值为4.
故答案为:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算,正确的是( )
A.x3x4=x12
B.(x3)3=x6
C.(3x)2=9x2
D.2x2÷x=x -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在8×6正方形方格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线
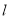 成轴对称的△AB′C′,并回答问题:
成轴对称的△AB′C′,并回答问题:图中线段CC′被直线l ;
(2)在直线l上找一点D,使线段DB+DC最短.(不写作法,应保留作图痕迹)
(3) 在直线l确定一点P,使得|PA-PB|的值最小.(不写作法,应保留作图痕迹)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是
A.a2+a3=a5B.a6÷a3=a2C.(a4)2=a6D.a2a3=a5
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,不能应用平方差公式进行计算的是( )
A.(-x+2y)(2y+x)B.(x+y)(x-y)C.(a-b)(-a+b)D.(-2m+n)(-2m-n)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=A1B,A1C=A1A2,A2D=A2A3,A3E=A3A4,∠B=20°,则∠A4=( )
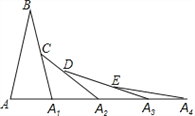
A. 10° B. 15° C. 30° D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边长分别为2和5,则该等腰三角形的周长为( )
A.7B.9C.9或12D.12
相关试题

