【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.
(1)求证:AE为⊙O的切线;
(2)当BC=4,AC=6时,求⊙O的半径;
(3)在(2)的条件下,求线段BG的长.

参考答案:
【答案】(1)见解析; (2) ![]() ;(3)1
;(3)1
【解析】试题分析:(1)连接OM,如图1,先证明OM∥BC,再根据等腰三角形的性质判断AE⊥BC,则OM⊥AE,然后根据切线的判定定理得到AE为⊙O的切线;
(2)设⊙O的半径为r,利用等腰三角形的性质得到BE=CE=![]() BC=2,再证明△AOM∽△ABE,则利用相似比得到
BC=2,再证明△AOM∽△ABE,则利用相似比得到![]() ,然后解关于r的方程即可;
,然后解关于r的方程即可;
(3)作OH⊥BE于H,如图,易得四边形OHEM为矩形,则HE=OM=![]() ,所以BH=BE-HE=
,所以BH=BE-HE=![]() ,再根据垂径定理得到BH=HG=
,再根据垂径定理得到BH=HG=![]() ,所以BG=1.
,所以BG=1.
试题解析:(1)证明:连接OM,如图1,
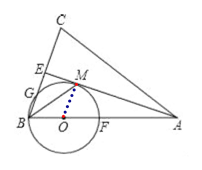
∵BM是∠ABC的平分线,
∴∠OBM=∠CBM,
∵OB=OM,
∴∠OBM=∠OMB,
∴∠CBM=∠OMB,
∴OM∥BC,
∵AB=AC,AE是∠BAC的平分线,
∴AE⊥BC,
∴OM⊥AE,
∴AE为⊙O的切线;
(2)解:设⊙O的半径为r,
∵AB=AC=6,AE是∠BAC的平分线,
∴BE=CE=![]() BC=2,
BC=2,
∵OM∥BE,
∴△AOM∽△ABE,
∴![]() ,即
,即![]() ,解得r=
,解得r=![]() ,
,
即设⊙O的半径为![]() ;
;
(3)解:作OH⊥BE于H,如图,
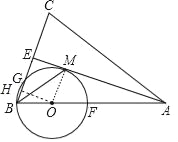
∵OM⊥EM,ME⊥BE,
∴四边形OHEM为矩形,
∴HE=OM=![]() ,
,
∴BH=BE﹣HE=2﹣![]() =
=![]() ,
,
∵OH⊥BG,
∴BH=HG=![]() ,
,
∴BG=2BH=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 为边
为边 上一点,
上一点, 为边
为边 的中点,过点
的中点,过点 作
作 ,交
,交 的延长线于点
的延长线于点 ,连结
,连结 .
.(1)求证:四边形
 是平行四边形;
是平行四边形;(2)若点
 为边
为边 的中点,当线段BC与线段AC满足什么数量关系时,四边形
的中点,当线段BC与线段AC满足什么数量关系时,四边形 为正方形.
为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2开始,连续的偶数相加,它们和的情况如下表:
加数的个数n
S
1
2=1×2
2
2+4=6=2×3
3
2+4+6=12=3×4
4
2+4+6+8=20=4×5
5
2+4+6+8+10=30=5×6
(1)若n=8时,则S的值为_____________.
(2)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=__________________.
(3)根据上题的规律计算2+4+6+8+10+…+98+100
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分别直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图
(2)求扇形统计图中m的值和E组对应的圆心角度数
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图2,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )

A. ① B. ② C. ①② D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )
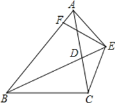
A.①②③B.①③④C.①②④D.①②③④
相关试题

