【题目】阅读下列材料:
在公式(a+1)2=a2+2a+1中,当a分别取1,2,3,4,…,n时,可得以下等式:
(1+1)2=12+2×1+1;
(2+1)2=22+2×2+1;
(3+1)2=32+2×3+1;
(4+1)2=42+2×4+1;
……
(n+1)2=n2+2n+1.
将这几个等式的左右两边分别相加,可以推导出求和公式:1+2+3+4+…+n=![]() .
.
请写出推导过程.
参考答案:
【答案】![]() ,推导过程见详解.
,推导过程见详解.
【解析】
将这n个等式的左右两边分别相加,然后将左右对应相等的项消去,将所得新的等式化简即可得到所求结论
解:左右两边分别相加,得
22+32+42+52+…+(n+1)2=12+22+32+42+…+n2+2(1+2+3+4+…+n)+n,
∴(n+1)2=1+2(1+2+3+4+…+n)+n,
即2(1+2+3+4+…+n)=n2+n,
∴1+2+3+4+…+n=![]() .
.
故答案为:![]() ,推导过程见详解.
,推导过程见详解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在半径为2cm的⊙O中,弦AB的长为2
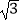 cm,则这条弦所对的圆周角为 .
cm,则这条弦所对的圆周角为 . -
科目: 来源: 题型:
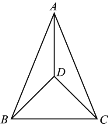
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是三角形内一点,连接AD,BD,CD,∠BDC=90°,∠DBC=45°.
(1)求证:∠BAD=∠CAD;
(2)求∠ADB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知C是线段AB垂直平分线m上一动点,连接AC,以AC为边作等边三角形ACD,点D在直线AB的上方,连接DB与直线m交于点E,连接BC,AE.
(1)如图1,点C在线段AB上.
①根据题意补全图1;
②求证:∠EAC=∠EDC;
(2)如图2,点C在直线AB的上方, 0°<∠CAB<30°,用等式表示线段BE,CE,DE之间的数量关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的线段AB及点P,给出如下定义:
若点P满足PA=PB,则称P为线段AB的“轴点”,其中,当0°<∠APB<60°时,称P为线段AB的“远轴点”;当60°≤∠APB≤180°时,称P为线段AB的“近轴点”.
(1)如图1,点A,B的坐标分别为(-2,0),(2,0),则在
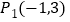 ,
, ,
, ,
, 中,线段AB的“近轴点”是 .
中,线段AB的“近轴点”是 .(2)如图2,点A的坐标为(3,0),点B在y轴正半轴上,且∠OAB=30°.
①若P为线段AB的“远轴点”,直接写出点P的横坐标t的取值范围 ;
②点C为y轴上的动点(不与点B重合且BC≠AB),若Q为线段AB的“轴点”,当线段QB与QC的和最小时,求点Q的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】布袋中有红、黄、蓝三种不同颜色的球各一个,从中先摸出一个球,记录下颜色后不放回布袋,将布袋搅匀,再摸出一个球,这时摸出的两个球是“一红一黄”的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABO.
(1)点A关于x轴对称的点的坐标为_________,点B关于y轴对称的点的坐标为_________;
(2)判断△ABO的形状,并说明理由.

相关试题

