Question

【题目】如图，二次函数y=ax2+bx+2（a≠0）的图象与x 轴交于A，B 两点，与y 轴交于点C，已知点 A(-4,0)，B(1,0)．

（1）求抛物线的解析式；

（2）若点 D(m,n) 是抛物线在第二象限的部分上的一动点，四边形 的面积为 ，求 关于 m 的函数关系；

（3）若点 E 为抛物线对称轴上任意一点，当以 A，C，E 为顶点的三角形是直角三角形时，请求出满足条件的所有点 E 的坐标．

Answer 1

【答案】（1）

（2）

（3）

【解析】试题解析：（1）用待定系数法求出函数解析式即可；（2）用m表示出点D的坐标，过点D作DH⊥x轴于点H，利用四边形OCDA的面积=△ADH的面积+ 四边形OCDH的面积即可求得S关于 m 的函数关系；（3）求出函数的对称轴，设出点E的坐标，分∠AEC=90°、

∠ACE=90°和∠CAE=90°三种情况求点E的坐标即可.

试题分析：

（1）∵A(-4,0)，B(1,0) 在二次函数y=ax2+bx+2（a≠0）的图象上，

∴ ， 解得 .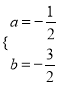

∴抛物线的解析式为．

（2）∵ 点D（m，n）是抛物线在第二象限的部分上的一动点，

∴D（m， ），

过点D作DH⊥x轴于点H，

则DH= ，AH=m+4，HO=-m，

∵ 四边形OCDA的面积=△ADH的面积+ 四边形OCDH的面积，

∴，

化简，得．

（3） 抛物线的对称轴为，

故设点E的坐标为（）．

∴．

若∠AEC=90°，则，

解得，

此时点E的坐标是或；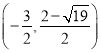

若∠ACE=90°，则，

解得n=5，此时点E的坐标是 ；

若∠CAE=90°，则，

解得 n=-5，此时点E的坐标是；

综上所述点E的坐标是或或或．