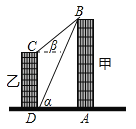
【题目】如图,线段AB、CD分别表示甲乙两建筑物的高,BA⊥AD,CD⊥DA,垂足分别为A、D.从D点测到B点的仰角α为60°,从C点测得B点的仰角β为30°,甲建筑物的高AB=30米
(1)求甲、乙两建筑物之间的距离AD.
(2)求乙建筑物的高CD.
参考答案:
【答案】(1)![]() ;(2)20.
;(2)20.
【解析】
试题分析:(1)在Rt△ABD中利用三角函数即可求解;
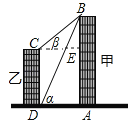
(2)作CE⊥AB于点E,在Rt△BCE中利用三角函数求得BE的长,然后根据CD=AE=AB﹣BE求解.
试题解析:(1)作CE⊥AB于点E,在Rt△ABD中,AD=![]() =
=![]() =
=![]() (米);
(米);
(2)在Rt△BCE中,CE=AD=![]() 米,BE=CEtanβ=
米,BE=CEtanβ=![]() ×
×![]() =10(米),则CD=AE=AB﹣BE=30﹣10=20(米)
=10(米),则CD=AE=AB﹣BE=30﹣10=20(米)
答:乙建筑物的高度DC为20m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CE是△ABC的角平分线,EF∥BC,交AC于点F.已知∠AFE=64°,则∠FEC的度数为( )
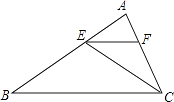
A.64°
B.32°
C.36
D.26° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B两地相距40千米,中午12:00时,甲从A地出发开车到B地,12:10时乙从B地出发骑自行车到A地,设甲行驶的时间为t(分),甲、乙两人离A地的距离S(千米)与时间t(分)之间的关系如图所示.由图中的信息可知,乙到达A地的时间为( )
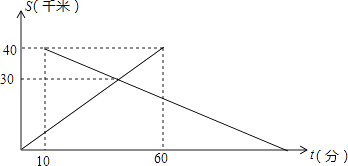
A.14:00 B.14:20 C.14:30 D.14:40 -
科目: 来源: 题型:
查看答案和解析>>【题目】为庆祝首个“中国农民丰收节”,海淀区将在海淀公园举办京西稻收割节活动,京西稻是著名农业作物,颗粒圆润,晶莹明亮,稻谷每粒重约0.000028千克.将0.000028用科学记数法表示为( )
A. 2.8×10﹣5B. 2.8×10﹣6C. 28×10﹣6D. 0.28×10﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】海南省是中国国土面积(含海域)第一大省,其中海域面积约为2000000平方公里,数据2000000用科学记数法表示为2×10n , 则n的值为( )
A.5
B.6
C.7
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,有一个边长为2个单位长度的等边△ABC,满足AC∥y轴.平移△ABC得到△A′B′C′,使点A′、B′分别在x轴、y轴上(不包括原点),则此时点C′的坐标是..
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角三角形中30°角所对的直角边为4cm,则斜边的长为__________cm.
相关试题

