【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:
事件A | 必然事件 | 随机事件 |
m的值 |
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于 ![]() ,求m的值.
,求m的值.
参考答案:
【答案】
(1)4,2,3
(2)解:根据题意得: ![]() =
= ![]() ,
,
解得:m=2,
所以m的值为2
【解析】解:(1)当袋子中全为黑球,即摸出4个红球时,摸到黑球是必然事件;
当摸出2个或3个时,摸到黑球为随机事件,
故答案为:4;2,3.
(1)根据随机事件及必然事件的定义即可得出答案;
(2)根据概率公式知:先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,摸出黑球的概率为![]() ,又知磁石的概率是
,又知磁石的概率是 ![]() ,从而列出方程,求解即可。
,从而列出方程,求解即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,直线AB:
 交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).
交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).(1)求直线AB的解析式和点B的坐标;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,求出点C的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.

(1)请用两种不同的方法求图2中阴影部分的面积.
方法1: ;
方法2: ;
(2)观察图2请你写出下列三个代数式:(m+n)2,(m-n)2,mn之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:
 ,
, ,求:
,求: 的值;
的值;②已知:
 ,
, ,求:
,求: 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:


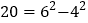
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为
 和
和 (其中
(其中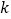 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由. (3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )
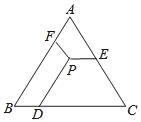
A. 18B. 9

C. 6D. 条件不够,不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】杭州地铁5号线全长48.18公里,投资315.9亿元,规划建设预期2014-2019年,杭州工程地铁队负责建设,分两个班组分别从杭州南站外香樟路站和余杭科技岛站同时开工掘进.已知甲组比乙组平均每天多掘进2.4米,经过5天施工,两组共掘进了110米.
(1)求甲、乙两个班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进1.7米,乙组平均每天能比原来多掘进1.3米.按此施工进度,能够比原来少用多少天完成任务?
相关试题

