【题目】如图,四边形ABCD内接于⊙O,BC是直径,∠BAD=120°,AB=AD.
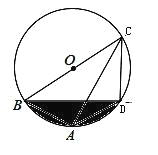
(1)求证:四边形ABCD是等腰梯形;
(2)已知AC=6,求阴影部分的面积.
参考答案:
【答案】(1)见解析 (2)4π-3![]()
【解析】试题分析:(1)根据AB=AD,∠BAD=120°可以得到∠ABD=∠ADB=30°,从而说明弧AB和弧AD的度数为60°,根据BC为直径可以说明弧CD的度数也是60°,从而可以得到AB=CD,然后根据∠CAD=∠ACB=30°得出AD∥BC;(2)阴影部分面积利用扇形面积减去△BOD的面积.
试题解析:(1)∵∠BAD=120°,AB=AD
∴∠ABD=∠ADB=30°
∴弧AB和弧AD的度数都等于60°
又 ∵BC是直径
∴弧CD的度数也是60°
∴AB=CD
∵∠CAD=∠ACB=30°
∴BC∥AD
∴四边形ABCD是等腰梯形.
(2)∵BC是直径
∴∠BAC=90°
∵∠ACB=30°,AC=6
∴BC=![]()
∴r=2![]()
∵弧AB和弧AD的度数都等于60°
∴∠BOD=120°
连接OA交BD于点E,则OA⊥BD
∴OE=OB×sin30°=![]() BE=0B×cos30°=3 BD=2BE=6
BE=0B×cos30°=3 BD=2BE=6
∴![]() =
=![]() =4π-3
=4π-3![]() .
.
-
科目: 来源: 题型:
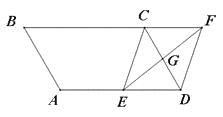
查看答案和解析>>【题目】(7分)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
-
科目: 来源: 题型:
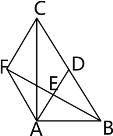
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1) 求证:AF=DC;
(2) 若AC⊥AB,试判断四边形ADCF的形状,并说明理由;
(3) 当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过平行四边形ABCD对角线交点O的直线交AD于E,交BC于F,若AB=5,BC=6,OE=2,那么四边形EFCD周长是( )
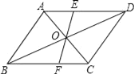
A. 16B. 15C. 14D. 13
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
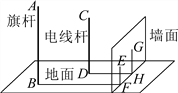
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如右图,在
 中,
中, ,
, ,垂足为点
,垂足为点 ,有下列说法:①点
,有下列说法:①点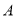 与点
与点 的距离是线段
的距离是线段 的长;②点
的长;②点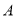 到直线
到直线 的距离是线段
的距离是线段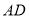 的长;③线段
的长;③线段 是
是 边
边 上的高;④线段
上的高;④线段 是
是 边
边 上的高.
上的高.上述说法中,正确的个数为( )

A. 1个B. 2个C. 3个D. 4个
相关试题

