【题目】如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
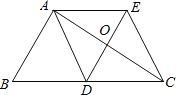
(1)求证:AD=EC;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)先证四边形ABDE是平行四边形,再证四边形ADCE是平行四边形,即得AD=CE;
(2)由∠BAC=90°,AD是边BC上的中线,即得AD=BD=CD,结合(1)知四边形ADCE是平行四边形,即证;
证明:(1)∵DE∥AB,AE∥BC,
∴四边形ABDE是平行四边形,
∴AE∥BD,且AE=BD
又∵AD是BC边的中线,
∴BD=CD,
∴AE=CD,
∵AE∥CD,
∴四边形ADCE是平行四边形,
∴AD=EC;
(2)∵∠BAC=90°,AD是斜边BC上的中线,
∴AD=BD=CD,
又∵四边形ADCE是平行四边形,
∴四边形ADCE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中 ①相反数等于本身的数是0,②绝对值等于本身的是正数,③倒数等于本身的数是±1,正确的个数为( )
A. 3个 B. 2个 C. 1个 D. 0个
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用分配律可以得﹣2×6+3×6=(﹣2+3)×6=﹣6.如果a表示任意一个有理数,那么利用分配律可以得到﹣2a+3a=(____)a=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把0.697按四舍五入法精确到0.01的近似值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,G是BC的中点,E是AG的中点,CE的延长线交AB于D,求AD:BD

(1)解:过G作GF∥AB,交CD于F.
请继续完成解答过程:
(2)创新求解:利用“杠杆平衡原理”
解答本题:(如图2)设G点为杠杆BC的支点,B端所挂物体质量为1Kg;则C端所挂物体质量为1Kg,G点承受质量为2Kg;当E点为杠杆AG的支点,则A端所挂物体质量为2Kg;
再以D为杠杆AB的支点时,AD:BD=1kg:2kg=1:2应用:如图3,在△ABC中,G是BC上一点,E是AG上一点,CE的延长线交AB于D,且
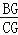 =
=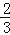 ,
,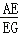 =2,求AD:BD
=2,求AD:BD解:设G点为杠杆BC的支点,B端所挂物体质量为6Kg,则C端所挂物体质量为 kg,G点承受质量为 kg;当E点为杠杆AG的支点,则A端所挂物体质量为 kg;再以D为杠杆AB的支点时,AD:BD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次射击练习中,某运动员命中的环数是7,9,9,10,10,其中9是( )
A. 平均数 B. 中位数 C. 众数 D. 既是平均数和中位数,又是众数
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ax2+2ax﹣3a= .
相关试题

