【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
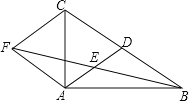
求证:(1)AF=CD;
(2)∠AFC=∠CDA.
参考答案:
【答案】证明见解析
【解析】
试题分析:(1)根据AAS证△AFE≌△DBE,推出AF=BD,即可得出答案;
(2)得出四边形ADCF是平行四边形,根据平行四边形的性质即可得到结论.
(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中
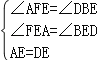
∴△AFE≌△DBE(AAS),
∴AF=BD,
∴AF=DC.
(2)证明:AF∥BC,AF=DC,
∴四边形ADCF是平行四边形,
∴∠AFC=∠CDA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】全班同学去春游,准备租船游玩,如果比计划减少一条船,则每条船正好坐9个同学,如果比计划增加一条船,每条船正好坐6个同学,则这个班有_____个同学,计划租用_____条船。
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程:3x+m=2的解也是方程:x- (1-x) =1的解,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解一路段车辆行驶速度的情况,交警统计了该路段上午7::0至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数、中位数分别是( )
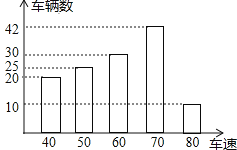
A.众数是80千米/时,中位数是60千米/时
B.众数是70千米/时,中位数是70千米/时
C.众数是60千米/时,中位数是60千米/时
D.众数是70千米/时,中位数是60千米/时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD和BE是△ABC的两条高,∠BCD=45°,BF=FC,BE与DF、DC分别交于点G、H,∠ACD=∠CBE.
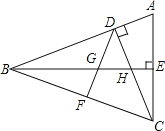
(1)判断△ABC的形状并说明理由;
(2)小明说:BH的长是AE的2倍.你认为正确吗?请说明理由.
(3)若BG=n2+1,GE=n2﹣1,求BH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是以PQ为底的等腰三角形时,运动的时间是( )
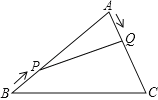
A.2.5秒 B.3秒 C.3.5秒 D.4秒
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A、平分弦的直径垂直于弦
B、三角形的外心到这个三角形的三边距离相等
C、相等的圆心角所对的弧相等
D、等弧所对的圆心角相等
相关试题

