【题目】如图,PA,PB是⊙O的两条切线,切点分别为A,B,OP交AB于点C,OP=13,sin∠APC= ![]() .
. 
(1)求⊙O的半径;
(2)求弦AB的长.
参考答案:
【答案】
(1)解:∵PA,PB是⊙O的两条切线,
∴∠OAP=90°,
∵sin∠APC= ![]() =
= ![]() ,OP=13,
,OP=13,
∴OA=5,
即所求半径为5
(2)解:Rt△OAP中,AP=12,
∵PA,PB是⊙O的两条切线,
∴PA=PB,∠APO=∠BPO,
∴PC⊥AB
由S四边形OAPB=S△OAP+S△OBP,得 ![]() OP×AB=OA×AP,
OP×AB=OA×AP,
∴AB= ![]() =
= ![]()
【解析】(1)由题意可推出OA⊥AP,即可推出OA的长度,即半径的长度;(2)根据题意和(1)的结论,即可推出PA=PB,∠APO=∠BPO,AC=BC= ![]() AB,可以推出AC的长度,即可推出AB的长度.
AB,可以推出AC的长度,即可推出AB的长度.
【考点精析】本题主要考查了切线的性质定理和解直角三角形的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据第5次、第6次人口普查的结果,2000年,2010年我国每10万人受教育程度的情况如下:

根据图中的信息,完成下列填空:
(1)2010年我国具有高中文化程度的人口比重为;
(2)2010年我国具有文化程度的人口最多;
(3)同2000年相比,2010年我国具有文化程度的人口增幅最大. -
科目: 来源: 题型:
查看答案和解析>>【题目】徐州至上海的铁路里程为650km.从徐州乘“C”字头列车A,“D”字头列车B都可到达上海,已知A车的平均速度为B车的2倍,且行驶时间比B车少2.5h.
(1)设A车的平均速度是xkm/h,根据题意,可列分式方程:;
(2)求A车的平均速度及行驶时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO. -
科目: 来源: 题型:
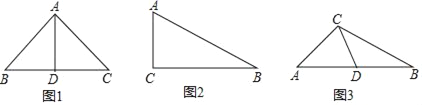
查看答案和解析>>【题目】定义:经过三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个三角形是等腰三角形,另外一个三角形和原三角形的三个内角分别相等,那么把这条线段定义为原三角形的“和谐分割线”.例如如图1:等腰直角三角形斜边上的中线就是一条“和谐分割线”.
(1)判断(对的打“√”,错的打“×”)
①等边三角形不存在“和谐分割线”
②如果三角形中有一个角是另一个角的两倍,则这个三角形必存在“和谐分割线”
(2)如图2,Rt△ABC,∠C=90°,∠B=30°,AC=2,请画出“和谐分割线”,并计算“和谐分割线”的长度;
(3)如图3,线段CD是△ABC的“和谐分割线”,∠A=42°,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD按如下的顺序进行折叠:对折,展平,得折痕EF(如图①);沿CG折叠,使点B落在EF上的点B′处,(如图②);展平,得折痕GC(如图③);沿GH折叠,使点C落在DH上的点C′处,(如图④);沿GC′折叠(如图⑤);展平,得折痕GC′,GH(如图 ⑥).

(1)求图 ②中∠BCB′的大小;
(2)图⑥中的△GCC′是正三角形吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,AB=AC,BC=acm,∠B=30°.动点P以1cm/s的速度从点B出发,沿折线B﹣A﹣C运动到点C时停止运动.设点P出发x s时,△PBC的面积为y cm2 . 已知y与x的函数图象如图②所示.请根据图中信息,解答下列问题:
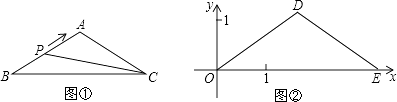
(1)试判断△DOE的形状,并说明理由;
(2)当a为何值时,△DOE与△ABC相似?
相关试题

