搜索
【题目】已知
，
，
，
满足
，
，则
__________．
参考答案：
【答案】60
【解析】
先利用单项式乘以多项式法则将要求值的多项式进行整理，将题目所给的有确定值的式子进行变形，得出所需要的式子的值，运用整体代入法既可求解．
∵m+n=p+q=4
∴（m+n）（p+q）=4×4=16
∵（m+n）（p+q）=mp+mq+np+nq
∴mp+mq+np+nq=16
∵mp+nq=6
∴mq+np=10
∴（m2+n2）pq+mn（p2+q2）
=m2pq+n2pq+mnp2+mnq2
=mpmq+npnq+mpnp+nqmq
=mpmq+mpnp+npnq+nqmq
=mp（mq+np）+np（nq+mq）
=（mp+nq）（np+mq）
=6×10
=60
故答案为：60
-
科目： 来源： 题型：
查看答案和解析>>【题目】南宁市青秀区新开发某工程准备招标，指挥部现接到甲、乙两个工程队的投标书，从投标书中得知：乙队单独完成这项工程所需天数是甲队单独完成这项工程所需天数的2倍；该工程若由甲队先做6天，剩下的工程再由甲、乙两队合作16天可以完成．
（1）求甲、乙两队单独完成这项工程各需要多少天？
（2）已知甲队每天的施工费用为0.67万元，乙队每天的施工费用为0.33万元，该工程预算的施工费用为19万元．为缩短工期，拟安排甲、乙两队同时开工合作完成这项工程，问：该工程预算的施工费用是否够用？若不够用，需要追加预算多少万元？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，以点C（1，1）为圆心，2为半径作圆，交x轴于A，B两点，点P在优弧
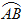上．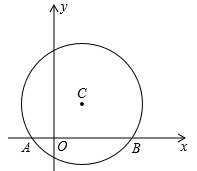
（1）求出A，B两点的坐标；
（2）试确定经过A、B且以点P为顶点的抛物线解析式；
（3）在该抛物线上是否存在一点D，使线段OP与CD互相平分？若存在，求出点D的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了解学生体育训练的情况，某市从全市九年级学生中随机抽取部分学生进行了一次体育科目测试（把测试结果分为四个等级：A级、B级、C级、D级），并将那个测试结果绘成了如下两幅不完整的统计图，请根据统计图中的信息解答下列问题：
（1）本次抽样测试的学生人数是 ；
（2）扇形图中∠α的度数是 ，并把条形统计图补充完整；
（3）对A，B，C，D四个等级依次赋分为90，75，65，55（单位：分），比如：等级为A的同学体育得分为90分，…，依此类推．该市九年级共有学生32000名，如果全部参加这次体育测试，估计该市九年级不及格（即60分以下）学生的人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料：
我们定义：若一个四边形的一条对角线把四边形分成两个等腰三角形，则这条对角线叫这个四边形的和谐线，这个四边形叫做和谐四边形．如正方形就是和谐四边形．结合阅读材料，完成下列问题：
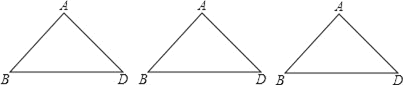
（1）下列哪个四边形一定是和谐四边形 ．
A．平行四边形 B．矩形 C．菱形 D．等腰梯形
（2）命题：“和谐四边形一定是轴对称图形”是 命题（填“真”或“假”）．
（3）如图，等腰Rt△ABD中，∠BAD＝90°．若点C为平面上一点，AC为凸四边形ABCD的和谐线，且AB＝BC，请求出∠ABC的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某家装公司聘请两队搬运工来搬运货物，他们都只能连续搬运5小时，甲队于某日0时开始搬运，过了1小时，乙队也开始搬运，如图，线段OG表示甲队搬运量y（千克）与时间x（时）的函数图象，线段EF表示乙队搬运量y（千克）与时间x（时）的函数图象．
（1）求乙队搬运量y与时间x之间的函数关系式．
（2）如果甲、乙两队各连续搬运5小时，那么乙队比甲队多搬运多少千克？
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料：一般地，
个相同的因数
相乘 
，记为
．如
，此时，
叫做以
为底
的对数，记为
（即
）．一般地，若
，（
且
，
），则叫做以为底
的对数，记为
（即
）．如
，则
叫做以为底
的对数，记为
（即
）．（1）计算以下各对数的值：
__________，
__________，
__________．（2）观察（1）中三数
、
，
之间满足怎样的关系式，
、
、
之间又满足怎样的关系式；（3）由（2）的结果，你能归纳出一个一般性的结论吗？
__________．（且，
，
）（4）根据幂的运算法则：
以及对数的含义证明上述结论．
相关试题
