【题目】如图,已知A(3,1),B(-2,3),线段AB与y轴相交于点C.

(1)求△AOB的面积;
(2)求点C的坐标;
(3)请直接写出直线AB与x轴的交点坐标.
参考答案:
【答案】(1)S△AOB=![]() ;(2)C(0,
;(2)C(0,![]() );(3)直线AB与x轴交点为(
);(3)直线AB与x轴交点为(![]() ,0);
,0);
【解析】
(1)过A作AE⊥x轴于E,过B作BF⊥x轴于F,S△AOB=S梯形AEFB-S△AOE-S△FOB=![]() -
-![]() -
-![]() =
=![]() ;
;
(2)S△AOB=S△AOC+S△COB,则有![]() =
=![]() OB×3+
OB×3+![]() ,即可求OC;
,即可求OC;
(3)设直线AB的解析式y=kx+b,将A(3,1),B(-2,3)代入,即可得y=-![]() x+
x+![]() ;
;
解:(1)过A作AE⊥x轴于E,过B作BF⊥x轴于F,
,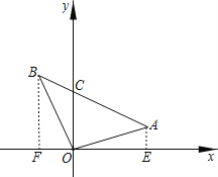
∵A(3,1),B(-2,3),
∴AE=1,BF=OE=3,FO=2,
∴EF=5,
∴S△AOB=S梯形AEFB-S△AOE-S△FOB=![]() -
-![]() -
-![]() =
=![]() ;
;
(2)∵S△AOB=S△AOC+S△COB,
∴![]() =
=![]() OB×3+
OB×3+![]() ,
,
∴OC=![]() ,
,
∴C(0,![]() );
);
(3)设直线AB的解析式y=kx+b,
将A(3,1),B(-2,3)代入,
∴![]() ,
,
∴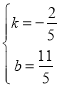 ,
,
∴y=-![]() x+
x+![]() ,
,
∴直线AB与x轴交点为(![]() ,0);
,0);
-
科目: 来源: 题型:
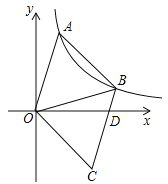
查看答案和解析>>【题目】(2017江苏省连云港市)如图,已知等边三角形OAB与反比例函数
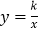 (k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则
(k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则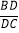 的值为____.(已知sin15°=
的值为____.(已知sin15°=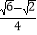 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆客车从甲地开往乙地,一辆轿车从乙地开往甲地,两车同时出发,两车行驶x小时后,记客车离甲地的距离为y1千米,轿车离甲地的距离为y2千米,y1、y2关于x的函数图象如图.
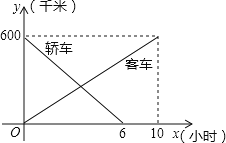
(1)根据图象,直接写出y1、y2关于x的函数关系式;
(2)当两车相遇时,求此时客车行驶的时间;
(3)两车相距200千米时,求客车行驶的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:
各版面选择人数的扇形统计图 各版面选择人数的条形统计图
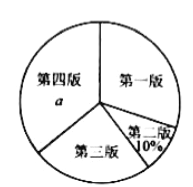

请根据图中信息,解答下列问题:
(1)该调查的样本容量为 ,

 ,“第一版”对应扇形的圆心角为
,“第一版”对应扇形的圆心角为  ;
; (2)请你补全条形统计图;
(3)若该校有
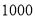 名学生,请你估计全校学生中最喜欢“第一版”的人数.
名学生,请你估计全校学生中最喜欢“第一版”的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.
组别
次数x
频数(人数)
A
80≤x<100
6
B
100≤x<120
8
C
120≤x<140
m
D
140≤x<160
18
E
160≤x<180
6
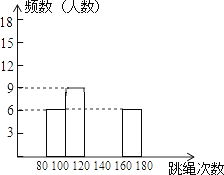
请结合图表解答下列问题:
(1)表中的m=________;
(2)请把频数分布直方图补完整;
(3)这个样本数据的中位数落在第________组;
(4)若九年级学生一分钟跳绳次数(x)合格要求是x≥120,则估计九年级学生中一分钟跳绳成绩不合格的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店决定购进A、B两种纪念品.若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B 种纪念品可获利润30元,在(2)的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
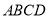 中,
中,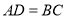 ,
,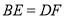 ,
,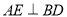 ,
,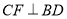 ,垂足分别为
,垂足分别为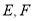 ,则四边形
,则四边形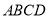 一定是( )
一定是( )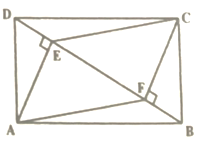
A. 正方形B. 菱形C. 平行四边形D. 矩形
相关试题

