【题目】如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )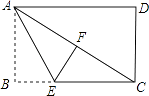
A.![]()
B.6
C.4
D.5
参考答案:
【答案】B
【解析】∵将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,
∴AF=AB,∠AFE=∠B=90°,
∴EF⊥AC,
∵∠EAC=∠ECA,
∴AE=CE,
∴AF=CF,
∴AC=2AB=6,
所以答案是:B.
【考点精析】掌握矩形的性质和翻折变换(折叠问题)是解答本题的根本,需要知道矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
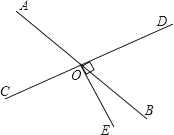
查看答案和解析>>【题目】如图,AB和CD相交于点O,∠DOE=90°,若∠BOE=
 ∠AOC,
∠AOC,(1)指出与∠BOD相等的角,并说明理由.
(2)求∠BOD,∠AOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC 的外接圆,AB=AC,BD是⊙O的直径,PA∥BC,与DB的延长线交于点P,连接AD.

(1)求证:PA是⊙O的切线;
(2)若AB= ,BC=4,求AD的长.
,BC=4,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】几何计算:
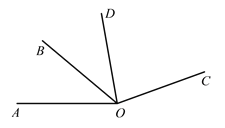
如图,已知∠AOB=40°,∠BOC=3∠AOB,OD平分∠AOC,求∠COD的度数.
解:因为∠BOC=3∠AOB,∠AOB=40°
所以∠BOC=__________°
所以∠AOC=__________ + _________
=__________° + __________°
=__________°
因为OD平分∠AOC
所以∠COD=
 __________=__________°
__________=__________°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
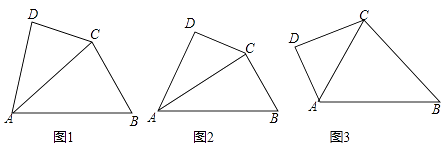
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 . -
科目: 来源: 题型:
查看答案和解析>>【题目】
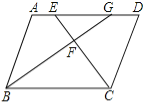
如图,已知:平行四边形ABCD中,∠BCD的平分线CE交边AD于E,∠ABC的平分线BG交CE于F,交AD于G.求证:AE=DG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.求证:
(1)BE=CF;
(2)四边形BECF是平行四边形.

相关试题

