【题目】如图,⊙O是△ABC 的外接圆,AB=AC,BD是⊙O的直径,PA∥BC,与DB的延长线交于点P,连接AD.
(1)求证:PA是⊙O的切线;
(2)若AB= ![]() ,BC=4,求AD的长.
,BC=4,求AD的长.
参考答案:
【答案】
(1)证明:连接OA交BC于点E,

由AB=AC可得OA⊥BC,
∵PA∥BC,
∴∠PAO=∠BEO=90°.
∵OA为⊙O的半径,
∴PA为⊙O的切线.
(2)解:根据(1)可得CE= ![]() BC=2.
BC=2.
Rt△ACE中, ![]() ,
,
∴tanC= ![]() .
.
∵BD是直径,
∴∠BAD=90°,
又∵∠D=∠C,
∴tanD= ![]() =
= ![]() ,
,
∴AD= ![]() .
.
【解析】(1)证PA是⊙O的切线,则需要证明PA垂直过A的半径,为此连接OA,利用垂径定理可证出OA⊥BC,再利用平行线的性质可得∠PAO=90°,可得证;
(2)在Rt△ACE中由勾股定理可求得AE的长,又![]() ,又易证∠D=∠C,且
,又易证∠D=∠C,且![]() ,从而求出AD的长.
,从而求出AD的长.
【考点精析】关于本题考查的勾股定理的概念和切线的判定定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我叫小白,你知道吗,2014年底南水北调中期工程开始运行,“南水”进京了,但是北京仍是特大型缺水城市,人均水资源量不到全国平均水平的
 .你了解吗,家庭中的冲水马桶是“大户”,用水量大约占家庭用水量的36%左右,两年前,我家每个月都要冲掉约3000升水.近两年来,我家使用新型冲水马桶,同时注意各种方法节水,现在我家全年用水量只有64000升,请你帮我算算,我家这两年用水的年平均下降率是多少?
.你了解吗,家庭中的冲水马桶是“大户”,用水量大约占家庭用水量的36%左右,两年前,我家每个月都要冲掉约3000升水.近两年来,我家使用新型冲水马桶,同时注意各种方法节水,现在我家全年用水量只有64000升,请你帮我算算,我家这两年用水的年平均下降率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=2
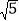 ,AC=4,BC=2,以AB为边向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长.
,AC=4,BC=2,以AB为边向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB和CD相交于点O,∠DOE=90°,若∠BOE=
 ∠AOC,
∠AOC,(1)指出与∠BOD相等的角,并说明理由.
(2)求∠BOD,∠AOD的度数.
-
科目: 来源: 题型:
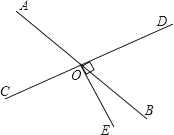
查看答案和解析>>【题目】几何计算:
如图,已知∠AOB=40°,∠BOC=3∠AOB,OD平分∠AOC,求∠COD的度数.
解:因为∠BOC=3∠AOB,∠AOB=40°
所以∠BOC=__________°
所以∠AOC=__________ + _________
=__________° + __________°
=__________°
因为OD平分∠AOC
所以∠COD=
 __________=__________°
__________=__________°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
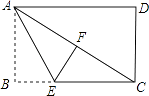
A.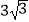
B.6
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
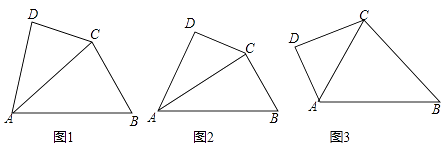
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
相关试题

