【题目】某中学为了了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图,请根图中提供的信息,解答下列问题:
(1)参加调查的人数共有 人;
(2)将条形图补充完整;
(3)求在扇形图中表示“其它球类”的扇形的圆心角的度数.

参考答案:
【答案】(1)300;(2)补全图形见解析;(3)在扇形图中表示“其它球类”的扇形的圆心角的度数为36°.
【解析】
(1)由乒乓球的人数及其所占百分比可得总人数;
(2)用总人数减去另外三种项目的人数求得足球的人数即可补全条形图;
(3)用360°乘以“其他球类”人数所占比例即可得.
解:(1)参加调查的总人数为60÷20%=300(人),
故答案为:300;
(2)足球的人数为300﹣(120+60+30)=90(人),
补全图形如下:

(3)在扇形图中表示“其它球类”的扇形的圆心角的度数为360°×![]() =36°.
=36°.
-
科目: 来源: 题型:
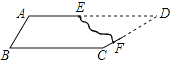
查看答案和解析>>【题目】有一块形状如图所示的玻璃,不小心把DEF部分打碎,现在只测得AB=60cm,BC=80cm,∠A=120°,∠B=60°,∠C=150°,你能设计一个方案,根据测得的数据求出AD的长吗?
-
科目: 来源: 题型:
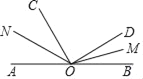
查看答案和解析>>【题目】如图,点O是直线AB上一点,OC⊥OD,OM是∠BOD的角平分线,ON是∠AOC的角平分线,则∠MON的度数是_____°.
-
科目: 来源: 题型:
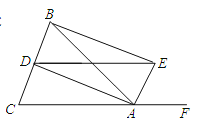
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD、AE分别是∠BAC与∠BAC的外角的平分线,BE⊥AE.求证:AB=DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处.
⑴若∠PEF=48°,点Q恰好落在其中的一条平行线上,则∠EFP的度数为 .
⑵若∠PEF=75°,∠CFQ=
 ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮从家步行到公交车站台,等公交车去学校. 图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是

A. 他离家8km共用了30min B. 他等公交车时间为6min
C. 他步行的速度是100m/min D. 公交车的速度是350m/min
-
科目: 来源: 题型:
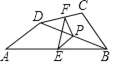
查看答案和解析>>【题目】如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,且∠A+∠ABC=90°,则∠PEF=_____.
相关试题

