【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A,B间的距离,有关他这次探究活动的描述错误的是( )
A.MN∥AB
B.AB=24m
C.△CMN∽△CAB
D.△CMN与四边形ABMN的面积之比为1:2
参考答案:
【答案】D
【解析】解:∵M、N分别是AC,BC的中点,
∴MN∥AB,MN=![]() AB,
AB,
∴AB=2MN=2×12=24m,△CMN∽△CAB,
∵M是AC的中点,
∴CM=MA,
∴CM:CA=1:2,
∴△CMN与△ACB的面积之比为1:4,
即△CMN与四边形ABMN的面积之比为1:3,
故描述错误的是D选项.
故选:D.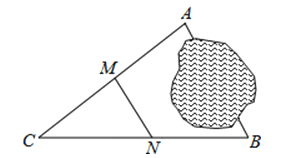
【考点精析】关于本题考查的三角形中位线定理,需要了解连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能得出正确答案.
-
科目: 来源: 题型:
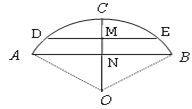
查看答案和解析>>【题目】一跨河桥,桥拱是圆弧形,跨度(AB)为12米,拱高(CN)为2米,求:
(1)桥拱半径;
(2)大雨过后,桥下河面宽度(DE)为10米,求水面涨高了多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:(1)无限小数是无理数;(2)无理数都是带根号的数;(3)任何实数都可以开立方;(4)有理数都是实数.其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,△TAB顶点坐标分别为T(1,1)、A(2,3)、B(4,2).
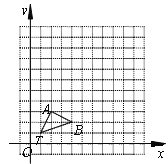
(1)以点T(1,1)为位似中心,按比例尺(TA′∶TA)3∶1在位似中心的同侧将△TAB放大为△TA′B′,放大后点A、B的对应点分别为A′、B′.画出△TA′B′,并写出点A′、B′的坐标;
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠1=42°13′,则∠1的余角是_____,补角是_____.
-
科目: 来源: 题型:
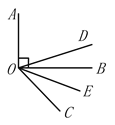
查看答案和解析>>【题目】如图,DO平分∠AOC,OE平分∠BOC,若OA⊥OB,
(1)当∠BOC=30°,∠DOE=_______________; 当∠BOC=60°,∠DOE=_______________;
(2)通过上面的计算,猜想∠DOE的度数与∠AOB有什么关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC向右平移4个单位长度,再向下平移5个单位长度,
(1)在图上画出对应的三角形A1B1C1;
(2)写出点A1、B1、C1的坐标.
(3)求出△A1B1C1的面积.
相关试题

