【题目】如图,反比例函数y= ![]() (x>0)的图象与矩形OABC对角线的交点为M,分别与AB,BC交于点D,E,连接OD,OE,则
(x>0)的图象与矩形OABC对角线的交点为M,分别与AB,BC交于点D,E,连接OD,OE,则 ![]() = , 当k=4时,四边形ODBE的面积为平方单位.
= , 当k=4时,四边形ODBE的面积为平方单位. 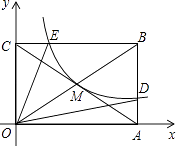
参考答案:
【答案】![]() ;12
;12
【解析】解:设B(a,b), ∴E( ![]() ,b),D(a,
,b),D(a, ![]() ),M(
),M( ![]() a,
a, ![]() b),
b),
∴k= ![]() a
a ![]() b=
b= ![]() ,
,
∴ab=4k,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ;
;
∵E、M、D位于反比例函数图象上,
则S△OCE= ![]() =2,S△OAD=
=2,S△OAD= ![]() =2,
=2,
过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=k,
又∵M为矩形ABCO对角线的交点,
∴S矩形ABCO=4S□ONMG=4k=16,
∴2+2+S四边形ODBE=16,
解得:S四边形ODBE=12.
所以答案是 ![]() ;12.
;12.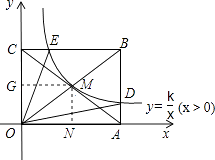
【考点精析】根据题目的已知条件,利用比例系数k的几何意义的相关知识可以得到问题的答案,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中的小方格都是边长为1的正方形,
①直接写出△ABC的各顶点坐标:
A(____,___),B(______,_______),C(______,_______);
②画出△ABC关于y轴的对称图形△A1B1C1;
③直接写出△ABC关于x轴对称的△A2B2C2的顶点A2(_____,____)B2(____,____)(其中A2与A对应,B2与B对应,不必画图.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多位自然数的任意两个相邻数位上,右边数位上的数总比左边数位上数大1,那么我们把这样的自然数叫做“相连数”.例如:234,4567,56789,…都是“相连数”.
(1)请直接写出最大的两位“相连数”与最小的三位“相连数”,并求它们的差.
(2)若某个“相连数”恰好等于其个位数的469倍,求这个“相连数”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列解题过程,然后解答问题
解方程:|x+3|=2.
解:当x+3≥0时,原方程可化为:x+3=2,解得x=﹣1
当x+3<0时,原方程可化为:x+3=﹣2,解得x=﹣5
所以原方程的解是x=﹣1,x=﹣5
(1)解方程:|3x﹣2|﹣4=0;
(2)探究:当b为何值时,方程|x﹣2|=b ①无解;②只有一个解;③有两个解.
(3)
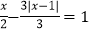
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司购买了一批A、B型芯片,其中A型芯片的单价比B型芯片的单价少9元,已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等.
(1)求该公司购买的A、B型芯片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条A型芯片?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费200元,生产一件B产品需加工费300元,应选择哪种生产方案,使生产这50件产品的成本最低?(成本=材料费+加工费)
-
科目: 来源: 题型:
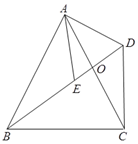
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
⑴ 求证:∠ABD=∠ACD;
⑵ 若∠ACB=65°,求∠BDC的度数.
相关试题

