搜索
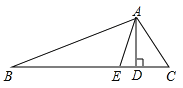
【题目】如图，在△ABC中，∠B=40°，∠C=60°，AD、AE分别是角平分线和高．求∠DAE的度数．
参考答案：
【答案】10°．
【解析】
试题分析：先根据三角形的内角和定理得到∠BAC的度数，再利用角平分线的性质可求出∠EAC=
∠BAC，而∠DAC=90°-∠C，然后利用∠DAE=∠EAC-∠DAC进行计算即可．
试题解析：在△ABC中，
∵∠B=40°，∠C=60°
∴∠BAC=180°-∠B-∠C=180°-40°-60°=80°
∵AE是的角平分线，
∴∠EAC=
∠BAC=×80°=40°，
∵AD是△ABC的高，
∴∠ADC=90°
∴在△ADC中，∠DAC=180°-∠ADC-∠C=180°-90°-60°=30°，
∴∠DAE=∠EAC-∠DAC=40°-30°=10°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一．为了增强居民的节水意识，某市自来水公司对居民用水采用以户为单位分段计费的办法收费．即一个月用水10吨以内（包括10吨）的用户，每吨收水费a元；一个月用水超过10吨的用户，10吨水仍按每吨a元收费，超过10吨的部分，按每吨b元（b＞a）收费．设一户居民月用水x吨，应收水费y元，y与x之间的函数关系如图
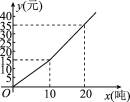
（1）求a的值，某户居民上月用水8吨，应收水费多少元；
（2）求b的值，并写出当x＞10时，y与x之间的函数关系式；
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，OC是∠AOM的平分线，OD是∠BOM的平分线．
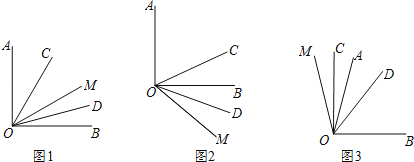
（1）如图1，若∠AOB=90°，∠AOM=60°，求∠COD的度数；
（2）如图2，若∠AOB=90°，∠AOM=130°，则∠COD= °；
（3）如图3，若∠AOB=m°，∠AOM=n°，则∠COD= °．
-
科目： 来源： 题型：
查看答案和解析>>【题目】【现场学习】
定义：我们把绝对值符号内含有未知数的方程叫做“含有绝对值的方程”．
如：|x|=2，|2x﹣1|=3，|
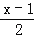|﹣x=1，…都是含有绝对值的方程．怎样求含有绝对值的方程的解呢？基本思路是：含有绝对值的方程→不含有绝对值的方程．
我们知道，根据绝对值的意义，由|x|=2，可得x=2或x=﹣2．
[例]解方程：|2x﹣1|=3．
我们只要把2x﹣1看成一个整体就可以根据绝对值的意义进一步解决问题．
解：根据绝对值的意义，得2x﹣1=3或2x﹣1= ．
解这两个一元一次方程，得x=2或x=﹣1．
检验：
（1）当x=2时，
原方程的左边=|2x﹣1|=|2×2﹣1|=3，
原方程的右边=3，
∵左边=右边
∴x=2是原方程的解．
（2）当x=﹣1时，
原方程的左边=|2x﹣1|=|2×（﹣1）﹣1|=3，
原方程的右边=3，
∵左边=右边
∴x=﹣1是原方程的解．
综合（1）（2）可知，原方程的解是：x=2，x=﹣1．
【解决问题】
解方程：|
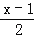|﹣x=1． -
科目： 来源： 题型：
查看答案和解析>>【题目】一次函数y＝(2m－6)x＋5中，y随x的增大而减小，则m的取值范围是 ________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若点A（﹣2，b）在第三象限，则点B（﹣b，4）在第象限_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两种商品原来的单价和为100元．因市场变化，甲商品降价10%，乙商品提价40%，调价后两种商品的单价和比原来的单价和提高了20%．甲、乙两种商品原来的单价各是多少？
相关试题
