【题目】如图,OC是∠AOM的平分线,OD是∠BOM的平分线.
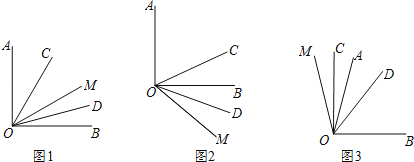
(1)如图1,若∠AOB=90°,∠AOM=60°,求∠COD的度数;
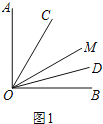
(2)如图2,若∠AOB=90°,∠AOM=130°,则∠COD= °;
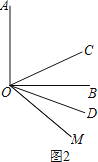
(3)如图3,若∠AOB=m°,∠AOM=n°,则∠COD= °.
参考答案:
【答案】(1)45°;(2)45;(3)![]() (m﹣n)°.
(m﹣n)°.
【解析】
试题分析:(1)直接利用角平分线的性质分别得出∠COM和∠DOM的值,进而得出答案;
(2)直接利用角平分线的性质分别得出∠COM和∠DOM的值,进而得出答案;
(3)直接利用角平分线的性质分别得出∠COM和∠DOM的值,进而得出答案.
解:(1)如图1,∵∠AOB=90°,∠AOM=60°,
∴∠BOM=∠AOB﹣∠AOM=90°﹣60°=30°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM=![]() ∠AOM=
∠AOM=![]() ×60°=30°,
×60°=30°,
∠DOM=![]() ∠BOM=
∠BOM=![]() ×30°=15°,
×30°=15°,
∴∠COD=∠COM+∠DOM=30°+15°=45°;
(2)如图2,∵∠AOB=90°,∠AOM=130°,
∴∠BOM=∠AOM﹣∠AOB=130°﹣90°=40°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM=![]() ∠AOM=
∠AOM=![]() ×130°=65°,
×130°=65°,
∠DOM=![]() ∠BOM=
∠BOM=![]() ×40°=20°,
×40°=20°,
∴∠COD=∠COM﹣∠DOM=65°﹣20°=45°
故答案为:45.
(3)如图3,∵∠AOB=m°,∠AOM=n°,
∴∠BOM=∠AOB+∠AOM=m°+n°,
∵OC是∠AOM的平分线,OD是∠BOM的平分线,
∴∠COM=![]() ∠AOM=
∠AOM=![]() ×n°=
×n°=![]() n°,
n°,
∠DOM=![]() ∠BOM=
∠BOM=![]() m°,
m°,
∴∠COD=∠DOM﹣∠COM=![]() m°﹣
m°﹣![]() n°=
n°=![]() (m﹣n)°.
(m﹣n)°.
故答案为:![]() (m﹣n)°.
(m﹣n)°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个有理数相除,其商是负数,则这两个有理数( )
A. 都是负数 B. 都是正数
C. 一个正数一个负数 D. 有一个是零
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.

(1)求证:△ABQ≌△CAP;
(2)如图1,当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说理由;若不变,求出它的度数.
(3)如图2,若点P、Q在分别运动到点B和点C后,继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC= 度.(直接填写度数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费的办法收费.即一个月用水10吨以内(包括10吨)的用户,每吨收水费a元;一个月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图
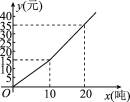
(1)求a的值,某户居民上月用水8吨,应收水费多少元;
(2)求b的值,并写出当x>10时,y与x之间的函数关系式;
-
科目: 来源: 题型:
查看答案和解析>>【题目】【现场学习】
定义:我们把绝对值符号内含有未知数的方程叫做“含有绝对值的方程”.
如:|x|=2,|2x﹣1|=3,|
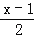 |﹣x=1,…都是含有绝对值的方程.
|﹣x=1,…都是含有绝对值的方程.怎样求含有绝对值的方程的解呢?基本思路是:含有绝对值的方程→不含有绝对值的方程.
我们知道,根据绝对值的意义,由|x|=2,可得x=2或x=﹣2.
[例]解方程:|2x﹣1|=3.
我们只要把2x﹣1看成一个整体就可以根据绝对值的意义进一步解决问题.
解:根据绝对值的意义,得2x﹣1=3或2x﹣1= .
解这两个一元一次方程,得x=2或x=﹣1.
检验:
(1)当x=2时,
原方程的左边=|2x﹣1|=|2×2﹣1|=3,
原方程的右边=3,
∵左边=右边
∴x=2是原方程的解.
(2)当x=﹣1时,
原方程的左边=|2x﹣1|=|2×(﹣1)﹣1|=3,
原方程的右边=3,
∵左边=右边
∴x=﹣1是原方程的解.
综合(1)(2)可知,原方程的解是:x=2,x=﹣1.
【解决问题】
解方程:|
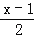 |﹣x=1.
|﹣x=1. -
科目: 来源: 题型:
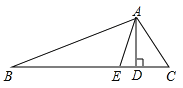
查看答案和解析>>【题目】如图,在△ABC中,∠B=40°,∠C=60°,AD、AE分别是角平分线和高.求∠DAE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=(2m-6)x+5中,y随x的增大而减小,则m的取值范围是 ________.
相关试题

