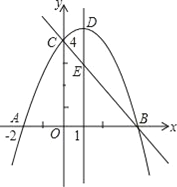
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
参考答案:
【答案】(1)、y=-![]()
![]() +x+4;(2)、不存在,理由见解析.
+x+4;(2)、不存在,理由见解析.
【解析】试题分析:(1)、首先设抛物线的解析式为一般式,将点C和点A意见对称轴代入求出函数解析式;(2)、本题利用假设法来进行证明,假设存在这样的点,然后设出点F的坐标求出FH和FG的长度,然后得出面积与t的函数关系式,根据方程无解得出结论.
试题解析:(1)、∵抛物线y=a![]() +bx+c(a≠0)过点C(0,4) ∴C=4①
+bx+c(a≠0)过点C(0,4) ∴C=4①
∵-![]() =1 ∴b=-2a② ∵抛物线过点A(-2,0) ∴4a-2b+c="0" ③
=1 ∴b=-2a② ∵抛物线过点A(-2,0) ∴4a-2b+c="0" ③
由①②③解得:a=-![]() ,b=1,c=4 ∴抛物线的解析式为:y=-
,b=1,c=4 ∴抛物线的解析式为:y=-![]()
![]() +x+4
+x+4
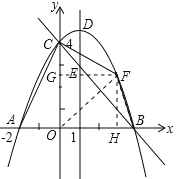
(2)、不存在 假设存在满足条件的点F,如图所示,连结BF、CF、OF,过点F作FH⊥x轴于点H,FG⊥y轴于点G. 设点F的坐标为(t, ![]() +t+4),其中0<t<4 则FH=
+t+4),其中0<t<4 则FH=![]() +t+4 FG=t
+t+4 FG=t
∴△OBF的面积=![]() OB·FH=
OB·FH=![]() ×4×(
×4×(![]() +t+4)=-
+t+4)=-![]() +2t+8 △OFC的面积=
+2t+8 △OFC的面积=![]() OC·FG=2t
OC·FG=2t
∴四边形ABFC的面积=△AOC的面积+△OBF的面积+△OFC的面积=-![]() +4t+12
+4t+12
令-![]() +4t+12=17 即-
+4t+12=17 即-![]() +4t-5=0 △=16-20=-4<0 ∴方程无解
+4t-5=0 △=16-20=-4<0 ∴方程无解
∴不存在满足条件的点F
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售A,B两种型号计算器,A型号计算器的进货价格为每台30元,B型号计算器的进货价格为每台40元.商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.
(1)分别求商场销售A,B两种型号计算器每台的销售价格.
(2)商场准备用不多于2 500元的资金购进A、B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?【利润=销售价格﹣进货价格】 -
科目: 来源: 题型:
查看答案和解析>>【题目】据调查,一部手机上的细菌平均可以达到600000000个,这个数字用科学记数法表示为( )
A.6×10
B.600×10
C.6×108
D.0.6×10 -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产的一批产品上市后30天内全部售完,调查发现,国内市场的日销售量为y1(吨)与时间t(t为整数,单位:天)的关系如图1所示的抛物线的一部分,而国外市场的日销售量y2(吨)与时间t,t为整数,单位:天)的关系如图2所示.
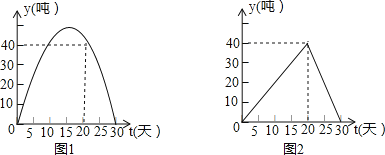
(1)求y1与时间t的函数关系式及自变量t的取值范围,并写出y2与t的函数关系式及自变量t的取值范围;
(2)设国内、国外市场的日销售总量为y吨,直接写出y与时间t的函数关系式,当销售第几天时,国内、外市场的日销售总量最早达到75吨?
(3)判断上市第几天国内、国外市场的日销售总量y最大,并求出此时的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.

(1)求证:AE=EF;
(2)如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,(1)中的结论是否仍然成立? ;(填“成立”或“不成立”);
(3)如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请证明,若不成立说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三个实数a、b、c满足a+b+c=0,a﹣b+c=0,则下列结论一定成立的是( )
A.a+b≥0B.a+c>0C.b+c≥0D.b2﹣4ac≥0
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
相关试题

