【题目】如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB=![]() ,抛物线y=ax2+bx经过点A(4,0)与点(﹣2,6).
,抛物线y=ax2+bx经过点A(4,0)与点(﹣2,6).
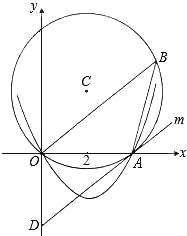
(1)求抛物线的函数解析式;
(2)直线m与⊙C相切于点A,交y轴于点D.动点P在线段OB上,从点O出发向点B运动;同时动点Q在线段DA上,从点D出发向点A运动;点P的速度为每秒一个单位长,点Q的速度为每秒2个单位长,当PQ⊥AD时,求运动时间t的值;
(3)点R在抛物线位于x轴下方部分的图象上,当△ROB面积最大时,求点R的坐标.
参考答案:
【答案】(1) y=![]() x2﹣2x.(2) t=1.8秒;(3) R(
x2﹣2x.(2) t=1.8秒;(3) R(![]() ,
,![]() ).
).
【解析】
试题分析:(1)根据抛物线y=ax2+bx经过点A(4,0)与点(﹣2,6),利用待定系数法求抛物线解析式;
(2)如图1,由已知条件,可以计算出OD、AE等线段的长度.当PQ⊥AD时,过点O作OF⊥AD于点F,此时四边形OFQP、OFAE均为矩形.则在Rt△ODF中,利用勾股定理求出DF的长度,从而得到时间t的数值;
(3)因为OB为定值,欲使△ROB面积最大,只需OB边上的高最大即可.按照这个思路解决本题.
如图2,当直线l平行于OB,且与抛物线相切时,OB边上的高最大,从而△ROB的面积最大.联立直线l和抛物线的解析式,利用一元二次方程判别式等于0的结论可以求出R点的坐标.
试题解析:(1)∵抛物线y=ax2+bx经过点A(4,0)与点(﹣2,6),
∴![]() ,
,
解得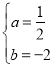
∴抛物线的解析式为:y=![]() x2﹣2x.
x2﹣2x.
(2)如图1,连接AC交OB于点E,由垂径定理得AC⊥OB.
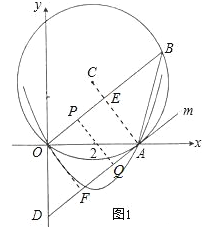
∵AD为切线,
∴AC⊥AD,
∴AD∥OB.
过O点作OF⊥AD于F,
∴四边形OFAE是矩形,
∵tan∠AOB=![]() ,
,
∴sin∠AOB=![]() ,
,
∴AE=OAsin∠AOB=4×![]() =2.4,
=2.4,
OD=OAtan∠OAD=OAtan∠AOB=4×![]() =3.
=3.
当PQ⊥AD时,OP=t,DQ=2t.
在Rt△ODF中,
∵OD=3,OF=AE=2.4,DF=DQ﹣FQ=DQ﹣OP=2t﹣t=t,
由勾股定理得:DF=![]() ,
,
∴t=1.8秒;
(3)如图2,设直线l平行于OB,且与抛物线有唯一交点R(相切),
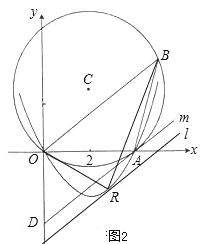
此时△ROB中OB边上的高最大,所以此时△ROB面积最大.
∵tan∠AOB=![]() ,∴直线OB的解析式为y=
,∴直线OB的解析式为y=![]() x,
x,
由直线l平行于OB,可设直线l解析式为y=![]() x+b.
x+b.
∵点R既在直线l上,又在抛物线上,
∴![]() x2﹣2x=
x2﹣2x=![]() x+b,化简得:2x2﹣11x﹣4b=0.
x+b,化简得:2x2﹣11x﹣4b=0.
∵直线l与抛物线有唯一交点R(相切),
∴判别式△=0,即112+32b=0,解得b=﹣![]() ,
,
此时原方程的解为x=![]() ,即xR=
,即xR=![]() ,
,
而yR=![]() xR2﹣2xR=
xR2﹣2xR=![]()
∴点R的坐标为R(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算2x6÷x4的结果是( )
A. x2 B. 2x2 C. 2x4 D. 2x10
-
科目: 来源: 题型:
查看答案和解析>>【题目】太阳的质量约为2.1×1027t,地球的质量约为6×1021t,则太阳的质量约是地球质量的( )
A. 3.5×106倍 B. 3.5×105倍
C. 3.5×107倍 D. 3.5×104倍
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量绘制的条形统计图如图.
比赛项目
票价(元/张)
男 篮
1000
足 球
800
乒乓球
x
依据上列图、表,回答下列问题:
(1)其中观看男篮比赛的门票有 张;观看乒乓球比赛的门票占全部门票的 %;
(2)公司决定采用随机抽取的方式把门票分配给100名员工,在看不到门票的条件下,每人抽取一张(假设所有的门票形状、大小、质地等完全相同且充分洗匀),问员工小亮抽到足球门票的概率是 ;
(3)若购买乒乓球门票的总款数占全部门票总款数的
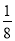 ,试求每张乒乓球门票的价格.
,试求每张乒乓球门票的价格.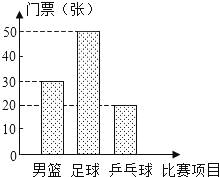
-
科目: 来源: 题型:
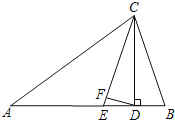
查看答案和解析>>【题目】如图所示,在△ABC中,∠A=38°,∠ABC=70°,CD⊥AB于点D,CE平分∠ACB,DF⊥CE于点F,求∠CDF的度数.
-
科目: 来源: 题型:
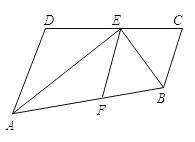
查看答案和解析>>【题目】如图,点E在线段CD上,EA、EB分别平分∠DAB和∠CBA,点F在线段AB上运动,AD=4cm,BC=3cm,且AD∥BC.
(1)你认为AE和BE有什么位置关系?并验证你的结论;
(2)当点F运动到离点A多少厘米时,△ADE和△AFE全等?为什么?
(3)在(2)的情况下,此时BF=BC吗?证明你的结论并求出AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+2b=0,则式子a3+2ab(a+b)+4b3的值是______.
相关试题

