【题目】如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,
(1)若∠A=40°,∠B=60°,求∠DCE的度数.
(2)若∠A=m,∠B=n,求∠DCE.(用m、n表示)

参考答案:
【答案】(1)10度;(2)![]()
【解析】试题分析:
(1)由已知易得∠ACB=80°,∠AEC=90°,由CD平分∠ACB可得∠ACD=40°,由∠AEC=90°、∠A=40°可得∠ACE=50°,这样就可得∠DCE=∠ACE-∠ACD=10°;
(2)把(1)中∠A=40°,∠B=60°分别换成m和n即可用含m、n的式子表达出∠DCE.
试题解析:
(1)∵△ABC中,∠A=40°,∠B=60°,
∴∠ACB=180°-40°-60°=80°,
又∵CD是∠ACB的角平分线,CE是AB边上的高,
∴∠ACD=![]() ∠ACB=40°,∠ACE=90°﹣∠A=50°,
∠ACB=40°,∠ACE=90°﹣∠A=50°,
∴∠DCE=∠ACE﹣∠ACD=50°﹣40°=10°;
(2)∵△ABC中,∠A=m,∠B=n,
∴∠ACB=180°﹣m﹣n,
又∵CD是∠ACB的角平分线,CE是AB边上的高,
∴∠ACD=![]() ∠ACB=
∠ACB=![]() ,∠ACE=90°﹣∠A=90°﹣m,
,∠ACE=90°﹣∠A=90°﹣m,
∴∠DCE=∠ACE﹣∠ACD=(90°﹣m)﹣![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:
①﹣|﹣ |=
|=
②﹣(﹣6)=
③(﹣1)99= . -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
①13+(﹣56)+47+(﹣34)
②( ﹣
﹣  ﹣
﹣  )×(﹣24)
)×(﹣24)
③(﹣1)10×2+(﹣2)3÷4
④﹣22+|5﹣8|+24÷(﹣3)× .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
①13+(﹣56)+47+(﹣34)
②( ﹣
﹣  ﹣
﹣  )×(﹣24)
)×(﹣24)
③(﹣1)10×2+(﹣2)3÷4
④﹣22+|5﹣8|+24÷(﹣3)× .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于P(a,b)和点Q(a,b′),给出如下定义:若b′=
 ,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(﹣2,5)的限变点的坐标是(﹣2,﹣5).
,则称点Q为点P的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(﹣2,5)的限变点的坐标是(﹣2,﹣5).(1)点(
 ,1)的限变点的坐标是 ;
,1)的限变点的坐标是 ;(2)判断点A(﹣2,﹣1)、B(﹣1,2)中,哪一个点是函数y=
 图象上某一个点的限变点?并说明理由;
图象上某一个点的限变点?并说明理由;(3)若点P(a,b)在函数y=﹣x+3的图象上,其限变点Q(a,b′)的纵坐标的取值范围是﹣6≤b′≤﹣3,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.

(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
-
科目: 来源: 题型:
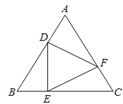
查看答案和解析>>【题目】如图,在等边三角形ABC的三边上,分别取点D,E,F,
使得△DEF为等边三角形,求证:AD=BE=CF.
相关试题

