【题目】为了考查学生的综合素质,九年级毕业生统一参加理化生实践操作科目考试。根据我市实际情况,市教育局决定:理化生实践考查科目命制24题,分4个试题单元,每个单元内含6道理化生实验操作题。即:物理3题;化学2题;生物1题。小聪与小明是某实验中学九年级的同班同学,在三月份举行的理化生考试中,他们同时抽到同一个试题单元,且每个同学都是同一个试题单元里随机抽取一题。
(1)小聪抽到物理学科科目可能性有多大?
(2)用列表法或树状图,求他俩同时抽到生物的概率是多少?
参考答案:
【答案】(1)P(小聪抽到物理学科)=![]() ;(2)
;(2)![]()
【解析】试题分析:(1)直接根据概率公式求解;
(2)首先根据题意列表得到所有可能,然后利用概率公式求解即可求得答案.
试题解析:解:(1)∵每个单元内含6道理化生实验操作题:物理3题;化学2题;生物1题,∴小聪抽到物理学科科目可能性=![]() =
=![]() ;
;
(2)设物理3题;化学2题;生物1题代号分别为1,2,3,4,5,6,列表得:

共有36种情况,两人同时抽到生物的情况有1种,即(6,6),所以他俩同时抽到生物的概率=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)计划购买这两种商品共50件,且投入的经费不超过3200元,那么,最多可购买多少件甲种商品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知四边形ABCD是正方形,对角线AC、BD相交于点E,以点E为顶点作正方形EFGH.
(1)如图1,点A、D分别在EH和EF上,连接BH、AF,直接写出BH和AF的数量关系;
(2)将正方形EFGH绕点E顺时针方向旋转.
①如图2,判断BH和AF的数量关系,并说明理由;
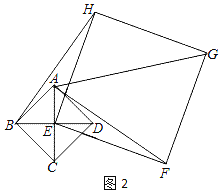
②如果四边形ABDH是平行四边形,请在备用图中补全图形;如果四方形ABCD的边长为
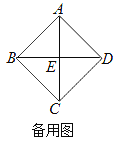
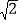 ,求正方形EFGH的边长.
,求正方形EFGH的边长.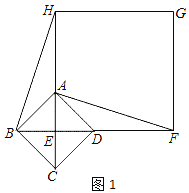
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(一6,8).矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.

(1)直接写出线段BO的长:
(2)求点D的坐标;
(3)若点N是平面内任一点,在x轴上是否存在点M,使咀M、N、E、O为顶点的四边形是菱形?若存在,请直接写出满足条件的点M的坐标:若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.在一条不完整的数轴上一动点A向左移动4个单位长度到达点B,再向右移动7个单位长度到达点C.

(1)若点A表示的数为0,求点B、点C表示的数;
(2)若点C表示的数为5,求点B、点A表示的数;
(3)如果点A、C表示的数互为相反数,求点B表示的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知B,C,E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F.求证:(1)△ACE≌△BCD;(2)
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读以下材料,完成下列问题.
(1)我们已经学过了乘方运算,我们知道表示2个-2相乘,即
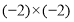 ,那么
,那么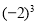 表示 ,把
表示 ,把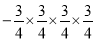 写成乘方的形式表示为 ,此时底数是 .
写成乘方的形式表示为 ,此时底数是 .(2)将(1)中两个底数同为-2的幂相乘,即
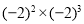 ,结果共有 个-2相乘,写成幂的形式为 ;
,结果共有 个-2相乘,写成幂的形式为 ;(3)若将(2)中算式中的底数都换为
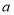 ,则
,则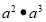 表示 ,计算结果为 .
表示 ,计算结果为 .若将(2)中算式中的指数换为正整数
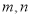 ,则
,则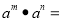 ,请用一句话概括你发现的结论 ;
,请用一句话概括你发现的结论 ;(4)利用上述结论,完成以下填空
若
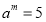 ,则
,则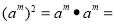 ,
,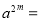 ;
;若
 ,
,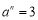 ,
,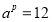 ,写出
,写出 的数量关系 .
的数量关系 .
相关试题

