【题目】如图,隧道的截面由抛物线AED和矩形ABCD(不含AD)构成.矩形的长BC为8 m,宽AB为2 m.以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6 m.
(1)求抛物线的函数表达式.
(2)如果该隧道内仅设双行道,现有一辆卡车高4.2 m,宽2.4 m,那么这辆卡车能否通过该隧道?

参考答案:
【答案】(1) y=-![]() x2+6. (2) 能通过该隧道.见解析.
x2+6. (2) 能通过该隧道.见解析.
【解析】分析:(1)根据抛物线在坐标系中的特殊位置,可以设抛物线的一般式,顶点式,求抛物线的解析式.(2)抛物线的实际应用问题中,可以取自变量的值,求函数值.
本题解析:
(1)由题意,得点E(0,6),D(4,2).
设抛物线的函数表达式为y=ax2+c,
则有![]() 解得
解得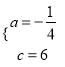
∴y=-![]() x2+6.
x2+6.
(2)当x=2.4时,y=-![]() ×2.42+6=4.56>4.2,∴这辆卡车能通过该隧道.
×2.42+6=4.56>4.2,∴这辆卡车能通过该隧道.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:8m﹣2m3=
-
科目: 来源: 题型:
查看答案和解析>>【题目】2020年我国考研人数约为340万,将340万这个数用科学记数法表示为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式成立的是( )
A.(-x-1)2=(x-1)2B.(-x-1)2=(x+1)2
C.(-x+1)2=(x+1)2D.(x+1)2=(x-1)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=x2+bx+5配方后为y=(x﹣2)2+k,则b+k= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P(
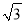 +1,
+1, 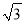 ﹣1)在双曲线y=kx-1(x>0)上.
﹣1)在双曲线y=kx-1(x>0)上.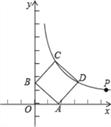
(1)求k的值;
(2)若正方形ABCD的顶点C,D在双曲线y=kx-1(x>0)上,顶点A,B分别在x轴和y轴的正半轴上,求点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△CDE,使得点D恰好落在AB上,连接BE,则BE的长度为 .
相关试题

