【题目】如图1,在△ABC中,∠B=90°,∠A=30°,AC=2.
(1)将△ABC绕点C顺时针旋转120°得△A′B′C.①求点B旋转经过的路径长;②求线段BB′的长;
(2)如图2,过点C作AC的垂线与AB的延长线交于点D,将△ACD绕点C顺时针旋转90°得△A′CD′.在图2中画出线段AD绕点C旋转所形成的图形(用阴影表示),并求出该图形的面积.

参考答案:
【答案】(1)![]() π;
π;![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)①由旋转的性质可知∠BCB′=120°,然后由扇形的弧长公式即可求得点B旋转经过的路径长;②由特殊锐角三角函数值可求得BB′的长;
(2)首先画出图形,然后根据S1=S2,可求得S1+S4的面积,然后再利用扇形面积-等边三角形ECD′的面积,从而可求得答案.
试题解析:(1)①∵AC=2,∠B=90°,∠A=30°,
∴BC=1.
∴点B旋转的路径=![]() ×2π×12=
×2π×12=![]() π;
π;
②如下图所示:
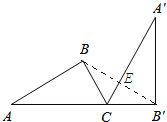
在△BCB′中,CB=CB′,∠BCB′=120°,AC⊥BB′
∴sin∠CBE=![]() .
.
∴BE=![]() .
.
∴BB′=![]() ;
;
(2)如图所示:

∵S1=S2,
∴S2+S4=S1+S4=![]() π(AC2-BC2)=
π(AC2-BC2)=![]() π(22-12)=
π(22-12)=![]() π.
π.
在Rt△ABD中,DC=ACtan30°=![]() ,
,
S3=![]() ×π×(
×π×(![]() )2-
)2-![]() ×
×![]() ×1=
×1=![]() π-
π-![]() ,
,
∴S2+S3+S4=![]() π+
π+![]() π-
π-![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算5x2-2x2的结果是( )
A. 3 B. 3x C. 3x2 D. 3x4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠D=50°,则下列结论:①∠AOE=65°;②OF平分∠BOD;③∠GOE=∠DOF;④∠GOE=25°。其中正确的是:( )
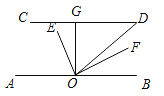
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有( )个
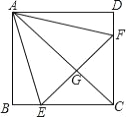
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】州教育局为了解我州八年级学生参加社会实践活动情况,随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据检测了两幅统计图,下面给出了两幅不完整的统计图(如图)
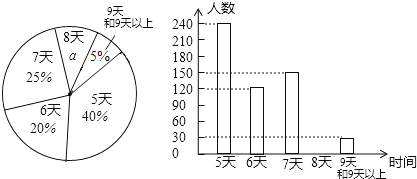
请根据图中提供的信息,回答下列问题:
(1)a= %,并写出该扇形所对圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该县共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①放大(缩小)的图片与原图片是相似形;
②比例尺不同的中国地图是相似形;
③放大镜下的五角星与原来的五角星是相似形;
④放电影时胶片上的图像和它映射到屏幕上的图像是相似形;
⑤平面镜中,你的像与你本人是相似形.
其中正确的说法有( )
A.2个
B.3个
C.4个
D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一元二次方程x2﹣2x+a=0有两个相等的实数根,则a的值是_____.
相关试题

