【题目】下图中表示一次函数 y mx n 与正比例函数 y nx(m , n 是常数,且 mn 0) 图象的是( )
A. B.
B. C.
C. D.
D.
参考答案:
【答案】B
【解析】
根据正比例函数的图象确定n的符号,然后由“两数相乘,同号得正,异号得负”判断出n的符号,再根据一次函数的性质进行判断.
A.根据图中正比例函数y=nx的图象知,n<0;
∵m,n是常数,且mn<0,
∴m>0,
∴一次函数y=mx+n的图象经过第一、三、四象限;
故本选项错误;
B.根据图中正比例函数y=nx的图象知,n>0;
∵m,n是常数,且mn<0,
∴m<0,
∴一次函数y=mx+n的图象经过第一、二、四象限;
故本选项正确;
C.根据图中正比例函数y=nx的图象知,n<0;
∵m,n是常数,且mn<0,
∴m>0,
∴一次函数y=mx+n的图象经过第一、三、四象限;
故本选项错误;
D.根据图中正比例函数y=nx的图象知,n>0;
∵m,n是常数,且mn<0,
∴m<0,
∴一次函数y=mx+n的图象经过第一、二、四象限;
故本选项错误;
故答案为:B.
-
科目: 来源: 题型:
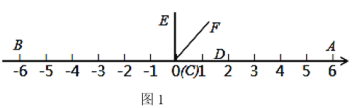
查看答案和解析>>【题目】如图1,在数轴上点A,点B对应的数分别是6,﹣6,∠DCE=90°(点C与点O重合,点D在数轴的正半轴上)
(1)如图1,若CF平分∠ACE,则∠AOF= 度;点A与点B的距离=
(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.

①当t=1时,α= ;点B与点C的距离=
②猜想∠BCE和α的数量关系,并说明理由;
(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0
 t
t 3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0
3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0 t
t 3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α﹣β|=20°,求t的值.
3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α﹣β|=20°,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在四边形ABCD中,∠A=∠C=90°.
(1)∠ABC+∠ADC= °;
(2)如图①,若DE平分∠ADC,BF平分∠ABC的外角,请写出DE与BF的位置关系,并证明;
(3)如图②,若BE,DE分别四等分∠ABC、∠ADC的外角(即∠CDE=
 ∠CDN,∠CBE=
∠CDN,∠CBE= ∠CBM),试求∠E的度数.
∠CBM),试求∠E的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校为了解学生对新闻、体育、动画、娱乐、戏曲类电视节目的喜爱情况,采用抽样的方法在七年级选取了一个班的同学,通过问卷调查,收集数据、整理数据,制作了如下两个整统计图,请根据下面两个不完整的统计图分析数据,回答以下问题:

(1)七年级的这个班共有学生_____人,图中
 ______,
______, ______,在扇形统计图中,“体育”类电视节目对应的圆心角为:______.
______,在扇形统计图中,“体育”类电视节目对应的圆心角为:______.(2)补全条形统计图;
(3)根据抽样调查的结果,估算该校1750名学生中大约有多少人喜欢“娱乐”类电视节目?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为 2 的正方形 ABCD 中剪去一个边长为 1 的小正方形 EFGD ,动点 P 从点 A 出发,沿A E F G C B 的路线,绕多边形的边匀速运动到点 B 时停止,则 ABP 的面积 S 随着时间t 变化的函数图象大致是( )

A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①、图②,在给定的一张矩形纸片上作一个正方形,甲、乙两人的作法如下:
甲:以点A为圆心,AD长为半径画弧,交AB于点E,以点D为圆心,AD长为半径画弧,交CD于点F,连接EF,则四边形AEFD即为所求;
乙:作∠DAB的平分线,交CD于点M,同理作∠ADC的平分线,交AB于点N,连接MN,则四边形ADMN即为所求.


对于以上两种作法,可以做出的判定是( )
A.甲正确,乙错误B.甲、乙均正确
C.乙正确,甲错误D.甲、乙均错误
相关试题

