【题目】某校八年级同学到距学校6千米的郊外秋游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往,如图,L1L2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数关系,则以下判断错误的是( )

A. 骑车的同学比步行的同学晚出发30分钟
B. 骑车的同学和步行的同学同时到达目的地
C. 骑车的同学从出发到追上步行的同学用了20分钟
D. 步行的速度是6千米/小时.
参考答案:
【答案】B
【解析】A. 由图知,骑车的同学比步行的同学晚出发30分钟,故A正确;
B. 由图知,骑车的同学比步行的同学先到达目的地,故B不正确;
C. 由图知, 骑车的同学从出发到追上步行的同学用了20分钟,故C正确;
D. 由图知,步行的速度是6千米/小时,故D正确;
故选B
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN
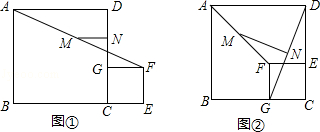
(1)线段MN和GD的数量关系是 , 位置关系是;
(2)将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;
(3)已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一块长方体木块的各棱长如图所示,一只蜘蛛在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处,蜘蛛急于捉住苍蝇,沿着长方体的表面向上爬.
(1)如果D是棱的中点,蜘蛛沿“AD→DB”路线爬行,它从A点爬到B点所走的路程为多少?
(2)你认为“AD→DB”是最短路线吗?如果你认为不是,请计算出最短的路程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形OABC的边长为2,顶点A,C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点,P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
(1)求点D的坐标(用含m的代数式表示);
(2)当△APD是以AP为腰的等腰三角形时,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+b经过点A(0,6),且平行于直线y=-2x.
(1)求该函数的解析式,并画出它的图象;
(2)如果这条直线经过点P(m,2),求m的值;
(3)若O为坐标原点,求直线OP的解析式;
(4)求直线y=kx+b和直线OP与坐标轴所围成的图形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0),B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.

(1)求该抛物线的解析式;
(2)一动点M从点D出发,以每秒1个单位的速度沿与y轴平行的方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?
(3)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某广电局与长江证券公司联合推出广电宽带网业务,用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务,用户缴纳上网费的方式有:方式一:每月80元包月;方式二:每月上网费y(元)与上网时间x(小时)的函数关系用如图所示的折线表示;方式三:以0小时为起点,每小时收费1.6元,月收费不超过120元.若设一用户每月上网x小时,月上网费为y元.

(1)根据图象,写出方式二中y(元)与x(小时)的函数关系式;
(2)试写出方式三中y(元)与x(小时)的函数关系式;
(3)若此用户每月上网60小时,选用哪种方式上网其费用最少?最少费用是多少?
相关试题

