【题目】如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN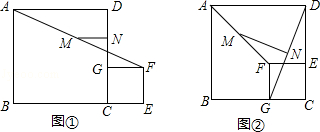
(1)线段MN和GD的数量关系是 , 位置关系是;
(2)将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;
(3)已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值.
参考答案:
【答案】
(1)MN= ![]() DG;MN⊥DG
DG;MN⊥DG
(2)
解:的结论仍然成立.
理由:过点M作MT⊥DC于T,过点M作MR⊥BC于R,连接FC、MD、MG,如图②,
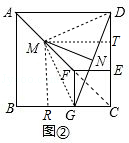
则A、F、C共线,MR∥FG∥AB,MT∥EF∥AD.
∵AM=FM,
∴BR=GR= ![]() BG,DT=ET=
BG,DT=ET= ![]() DE,
DE,
∴MR= ![]() (FG+AB),MT=
(FG+AB),MT= ![]() (EF+AD).
(EF+AD).
∵四边形ABCD和四边形EFGC都是正方形,
∴FG=GC=EC=EF,AB=BC=DC=AD,
∴MR=MT,RG=TD.
在△MRG和△MTD中,
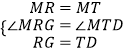 ,
,
∴△MRG≌△MTD,
∴MG=MD,∠RMG=∠TMD,
∴∠RMT=∠GMD.
∵∠MRC=∠RCT=∠MTC=90°,
∴四边形MRCT是矩形,
∴∠RMT=90°,
∴∠GMD=90°.
∵MG=MD,∠GMD=90°,DN=GN,
∴MN⊥DG,MN= ![]() DG.
DG.
(3)
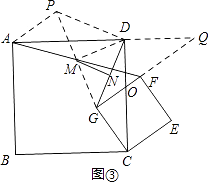
解:延长GM到点P,使得PM=GM,延长GF、AD交于点Q,连接AP,DP,DM如图③,
在△AMP和△FMG中,
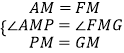 ,
,
∴△AMP≌△FMG,
∴AP=FG,∠APM=∠FGM,
∴AP∥GF,
∴∠PAQ=∠Q,
∵∠DOG=∠ODQ+∠Q=∠OGC+∠GCO,
∠ODQ=∠OGC=90°,
∴∠Q=∠GCO,
∴∠PAQ=∠GCO.
∵四边形ABCD和四边形EFGC都是正方形,
∴DA=DC,GF=GC,
∴AP=CG.
在△APD和△CGD中,
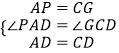 ,
,
∴△APD≌△CGD,
∴PD=DG.
∵PM=GM,
∴DM⊥PG.
∵DN=GN,
∴MN= ![]() DG.
DG.
∵GC=CE=3,
∴点G在以点C为圆心,3为半径的圆上,
∵DC=BC=7,
∴DG的最大值为7+3=10,最小值为7﹣3=4,
∴MN的最大值为5,最小值为2.
【解析】解:(1)连接FN并延长,与AD交于点S,如图①.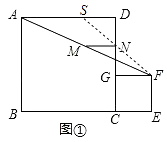
∵四边形ABCD和四边形EFGC都是正方形,
∴∠D=90°,AD=DC,GC=GF,AD∥BE∥GF,
∴∠DSN=∠GFN.
在△SDN和△FGN中,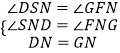 ,
,
∴△SDN≌△FGN,
∴DS=GF,SN=FN.
∵AM=FM,
∴MN∥AS,MN= ![]() AS,
AS,
∴∠MNG=∠D=90°,
MN= ![]() (AD﹣DS)=
(AD﹣DS)= ![]() (DC﹣GF)=
(DC﹣GF)= ![]() (DC﹣GC)=
(DC﹣GC)= ![]() DG.
DG.
故答案为MN= ![]() DG,MN⊥DG;
DG,MN⊥DG;
(1)连接FN并延长,与AD交于点S,如图①,易证△SDN≌△FGN,则有DS=GF,SN=FN,然后运用三角形中位线定理就可解决问题;(2)过点M作MT⊥DC于T,过点M作MR⊥BC于R,连接FC、MD、MG,如图②,根据平行线分线段成比例可得BR=GR= ![]() BG,DT=ET=
BG,DT=ET= ![]() DE,根据梯形中位线定理可得MR=
DE,根据梯形中位线定理可得MR= ![]() (FG+AB),MT=
(FG+AB),MT= ![]() (EF+AD),从而可得MR=MT,RG=TD,由此可得△MRG≌△MTD,则有MG=MD,∠RMG=∠TMD,则有∠RMT=∠GMD,进而可证到△DMG是等腰直角三角形,然后根据等腰三角形的性质和直角三角形斜边上的中线等于斜边的一半,就可解决问题;(3)连接GM到点P,使得PM=GM,延长GF、AD交于点Q,连接AP,DP,DM如图③,易证△APD≌△CGD,则有PD=DG,根据等腰三角形的性质可得DM⊥PG,根据直角三角形斜边上的中线等于斜边的一半可得MN=
(EF+AD),从而可得MR=MT,RG=TD,由此可得△MRG≌△MTD,则有MG=MD,∠RMG=∠TMD,则有∠RMT=∠GMD,进而可证到△DMG是等腰直角三角形,然后根据等腰三角形的性质和直角三角形斜边上的中线等于斜边的一半,就可解决问题;(3)连接GM到点P,使得PM=GM,延长GF、AD交于点Q,连接AP,DP,DM如图③,易证△APD≌△CGD,则有PD=DG,根据等腰三角形的性质可得DM⊥PG,根据直角三角形斜边上的中线等于斜边的一半可得MN= ![]() DG.要求MN的最大值和最小值,只需求DG的最大值和最小值,由GC=CE=3可知点G在以点C为圆心,3为半径的圆上,再由DC=BC=7,就可求出DG的最大值和最小值.
DG.要求MN的最大值和最小值,只需求DG的最大值和最小值,由GC=CE=3可知点G在以点C为圆心,3为半径的圆上,再由DC=BC=7,就可求出DG的最大值和最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图2,“和谐号”高铁列车的小桌板收起时近似看作与地面垂直,展开小桌板使桌面保持水平时如图1,小桌板的边沿O点与收起时桌面顶端A点的距离OA=75厘米,此时CB⊥AO,∠AOB=∠ACB=37°,且支架长OB与支架长BC的长度之和等于OA的长度.

(1)求∠CBO的度数;
(2)求小桌板桌面的宽度BC.(参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75) -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家樱桃采摘园的品质相同,销售价格也相同,“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
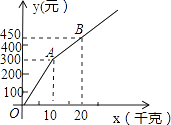
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克元;
(2)求y1、y2与x的函数表达式;
(3)在图中画出y1与x的函数图象,若某人想在“五一期间”采摘樱桃25千克,那么甲、乙哪个采摘园较为优惠?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=
 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=  ,OB=4,OE=2.
,OB=4,OE=2. 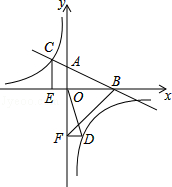
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】一块长方体木块的各棱长如图所示,一只蜘蛛在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处,蜘蛛急于捉住苍蝇,沿着长方体的表面向上爬.
(1)如果D是棱的中点,蜘蛛沿“AD→DB”路线爬行,它从A点爬到B点所走的路程为多少?
(2)你认为“AD→DB”是最短路线吗?如果你认为不是,请计算出最短的路程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形OABC的边长为2,顶点A,C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点,P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
(1)求点D的坐标(用含m的代数式表示);
(2)当△APD是以AP为腰的等腰三角形时,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级同学到距学校6千米的郊外秋游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往,如图,L1L2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数关系,则以下判断错误的是( )

A. 骑车的同学比步行的同学晚出发30分钟
B. 骑车的同学和步行的同学同时到达目的地
C. 骑车的同学从出发到追上步行的同学用了20分钟
D. 步行的速度是6千米/小时.
相关试题

