【题目】如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.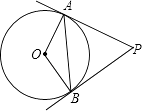
(1)求∠APB的度数;
(2)当OA=3时,求AP的长.
参考答案:
【答案】
(1)解:方法一:
∵在△ABO中,OA=OB,∠OAB=30°,
∴∠AOB=180°﹣2×30°=120°,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,即∠OAP=∠OBP=90°,
∴在四边形OAPB中,
∠APB=360°﹣120°﹣90°﹣90°=60°.
方法二:
∵PA、PB是⊙O的切线∴PA=PB,OA⊥PA;
∵∠OAB=30°,OA⊥PA,
∴∠BAP=90°﹣30°=60°,
∴△ABP是等边三角形,
∴∠APB=60°
(2)解:方法一:如图①,连接OP;
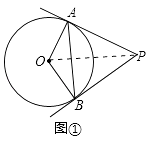
∵PA、PB是⊙O的切线,
∴PO平分∠APB,即∠APO= ![]() ∠APB=30°,
∠APB=30°,
又∵在Rt△OAP中,OA=3,∠APO=30°,
∴AP= ![]() =3
=3 ![]() .
.
方法二:如图②,作OD⊥AB交AB于点D;
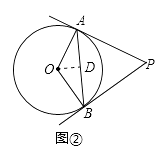
∵在△OAB中,OA=OB,
∴AD= ![]() AB;
AB;
∵在Rt△AOD中,OA=3,∠OAD=30°,
∴AD=OAcos30°= ![]() ,
,
∴AP=AB= ![]() .
.
【解析】(1) 方法一: 根据等边对等角及三角形的内角和得出∠AOB,再根据切线的性质及四边形的内角和得出答案;方法二:根据切线的性质及余角的定义得出△ABP是等边三角形,,从而得出结论;(2)方法一:如图①,连接OP; 利用切线的性质得出∠APO=30°,在Rt△OAP中,AP=![]() ,方法二:如图②,作OD⊥AB交AB于点D;根据等腰三角形的三线合一得出AD=
,方法二:如图②,作OD⊥AB交AB于点D;根据等腰三角形的三线合一得出AD= ![]() AB,在Rt△AOD中,AD=OAcos30°,从而得出结论。
AB,在Rt△AOD中,AD=OAcos30°,从而得出结论。
-
科目: 来源: 题型:
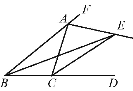
查看答案和解析>>【题目】如图,A,B两点分别表示两幢大楼所在的位置,直线a表示输水总管道,直线b表示输煤气总管道.现要在这两根总管道上分别设一个连接点,安装分管道将水和煤气输送到A,B两幢大楼,要求使铺设至两幢大楼的输水分管道和输煤气分管道的用料最短.图中,点A'是点A关于直线b的对称点,A'B分别交直线b,a于点C,D;点B'是点B关于直线a的对称点,B'A分别交直线b,a于点E,F.则符合要求的输水和输煤气分管道的连接点依次是
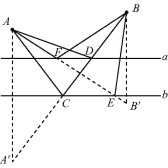
A. F和C B. F和E C. D和C D. D和E
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.

(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BE平分∠ABC,CE平分∠ACD,且交BE于点E,∠BAC=30°,则∠CAE=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B,C两地相距120海里.
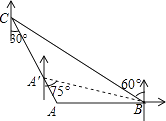
(1)求出此时点A到岛礁C的距离;
(2)若“中海监50”从A处沿AC方向向岛礁C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时“中国海监50”的航行距离.(注:结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,△ABC的三个顶点A、B、C都在格点上.
(1)在图中画出与△ABC关于直线l成轴对称的△A1B1C1;
(2)在直线l上找出一点P,使得|PA﹣PC|的值最大;(保留作图痕迹并标上字母P)
(3)在直线l上找出一点Q,使得QA+QC1的值最小;(保留作图痕迹并标上字母Q)
(4)在正方形网格中存在 个格点,使得该格点与B、C两点构成以BC为底边的等腰三角形.

-
科目: 来源: 题型:
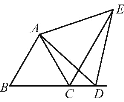
查看答案和解析>>【题目】如图,点B,C,D在一条直线上,△ABC,△ADE是等边三角形,若CE=15cm,CD=6cm,则AC=__,∠ECD=__.
相关试题

