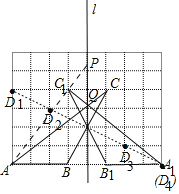
【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,△ABC的三个顶点A、B、C都在格点上.
(1)在图中画出与△ABC关于直线l成轴对称的△A1B1C1;
(2)在直线l上找出一点P,使得|PA﹣PC|的值最大;(保留作图痕迹并标上字母P)
(3)在直线l上找出一点Q,使得QA+QC1的值最小;(保留作图痕迹并标上字母Q)
(4)在正方形网格中存在 个格点,使得该格点与B、C两点构成以BC为底边的等腰三角形.

参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析;(4)4
【解析】
(1)分别作出A,B,C的对应点A1,B1,C1即可;
(2)连接AC1,延长AC1交直线l于点P,点P即为所求;
(3)直线AC与直线l的交点Q即为所求;
(4)作线段BC的垂直平分线,如图D1,D2,D3,D4即为所求.
解:(1)△A1B1C1如图所示,
由对称的性质,分别作出A,B,C的对应点A1,B1,C1,顺次连结A1B1,A1 C1,B1C1,
得到△A1B1C1与△ABC关于直线l成轴对称;
(2)∵C与C1关于直线l对称,
∴PC=PC1,
∴|PA﹣PC|=|PA﹣PC1|,当P、A、C1三点共线时,|PA﹣PC1|取得最大值,即|PA﹣PC|的值最大,
∴连接AC1,延长AC1交直线l于点P,点P即为所求;
(3)∵C与C1关于直线l对称,
∴QC=QC1,
∴QA+QC1=QA+QC,当A、Q、C三点共线时,QA+QC取得最小值,即QA+QC1的值最小;
∴直线AC与直线l的交点Q即为所求;
(4)∵构成以BC为底边的等腰三角形,
则等腰三角形的顶点在线段BC的垂直平分线上,
∴作线段BC的垂直平分线,如图D1,D2,D3,D4即为所求,共4个格点;
故答案为4.
-
科目: 来源: 题型:
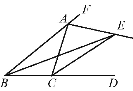
查看答案和解析>>【题目】如图,已知BE平分∠ABC,CE平分∠ACD,且交BE于点E,∠BAC=30°,则∠CAE=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.
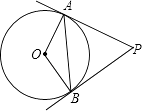
(1)求∠APB的度数;
(2)当OA=3时,求AP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B,C两地相距120海里.
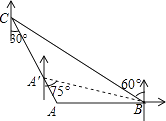
(1)求出此时点A到岛礁C的距离;
(2)若“中海监50”从A处沿AC方向向岛礁C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时“中国海监50”的航行距离.(注:结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B,C,D在一条直线上,△ABC,△ADE是等边三角形,若CE=15cm,CD=6cm,则AC=__,∠ECD=__.
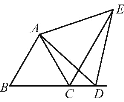
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线分别交AB于点F,交BC的延长线于点E.
求证:(1)∠EAD=∠EDA;
(2)DF∥AC.
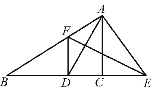
-
科目: 来源: 题型:
查看答案和解析>>【题目】(A类)已知如图,四边形ABCD中,AB=BC,AD=CD,求证:∠A=∠C.
(B类)已知如图,四边形ABCD中,AB=BC,∠A=∠C,求证:AD=CD.
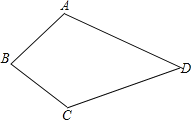
相关试题

