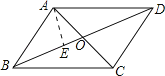
【题目】平行四边形ABCD中,对角线AC、BD交于点O,若∠BOC=120°,AD=7,BD=10,则平行四边形ABCD的面积为 .
参考答案:
【答案】15![]() .
.
【解析】
试题分析:过点A作AE⊥BD于E,设OE=a,则AE=![]() a,OA=2a,在直角三角形ADE中,利用勾股定理可得DE2+AE2=AD2,进而可求出a的值,△ABD的面积可求出,由平行四边形的性质可知:ABCD的面积=2S△ABD,问题得解.
a,OA=2a,在直角三角形ADE中,利用勾股定理可得DE2+AE2=AD2,进而可求出a的值,△ABD的面积可求出,由平行四边形的性质可知:ABCD的面积=2S△ABD,问题得解.
解:过点A作AE⊥BD于E,
∵四边形ABCD是平行四边形,
∴OD=![]() BD=
BD=![]() ×10=5,
×10=5,
∵∠BOC=120°,
∴∠AOE=60°,
设OE=a,则AE=![]() a,OA=2a,
a,OA=2a,
∴DE=5+a,
在直角三角形ADE中,由勾股定理可得DE2+AE2=AD2,
∴(5+a)2+(![]() a)2=72,
a)2=72,
解得:a=![]() ,
,
∴AE=![]() ×
×![]() =
=![]() ,
,
∴ABCD的面积=2S△ABD=2×10×![]() ×
×![]() =15
=15![]() .
.
故答案为:15![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.
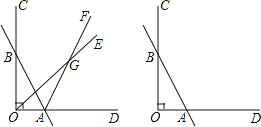
(1)若OE平分∠BOA,AF平分∠BAD,∠OBA=30°,则∠OGA= .
(2)若∠GOA=
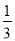 ∠BOA,∠GAD=
∠BOA,∠GAD=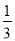 ∠BAD,∠OBA=30°,则∠OGA= .
∠BAD,∠OBA=30°,则∠OGA= .(3)将(2)中“∠OBA=30°”改为“∠OBA=α”,其余条件不变,则∠OGA= (用含α的代数式表示)
(4)若OE将∠BOA分成1:2两部分,AF平分∠BAD,∠ABO=α(30°<α<90°),求∠OGA的度数(用含α的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B在反比例函数
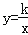 的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,
的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,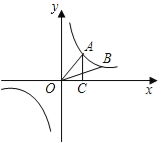
(1)求该反比例函数的解析式;
(2)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.求证:ADBC=APBP.
(2)探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=12,AD=BD=10.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切,求t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个角的补角等于这个角的余角的4倍,则这个角的度数是( )
A. 30° B. 60° C. 90° D. 120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一组数据:1,3,3,4,5,这组数据的众数为( )
A.1 B.3 C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子里装有若干个红球和黄球,这些球除颜色外完全相同.从中任意摸出一个球,记下颜色后放回,搅匀后再重新摸球,则下列说法中正确的是( )
A.摸到黄球的频数越大,摸到黄球的频率越大
B.摸到黄球的频数越大,摸到黄球的频率越小
C.重复多次摸球后,摸到黄球的频数逐渐稳定
D.重复多次摸球后,摸到黄球的频率逐渐稳定
相关试题

